10-3:3次ベジェ曲線の当たり判定式
3次ベジェ曲線の当たり判定デモはこんな感じです。
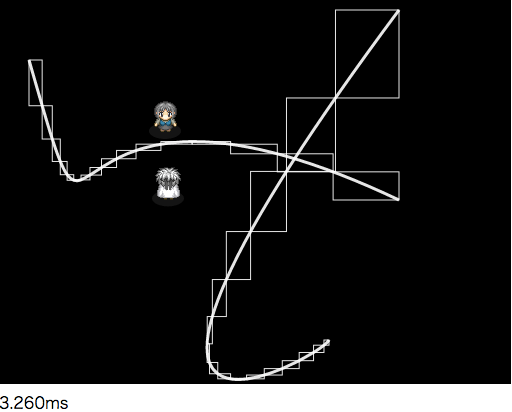
⇒ 3次ベジェ曲線とキャラクター(矩形)の当たり判定デモを見る
3次ベジェ曲線と矩形の当たり判定を考える
(2019.4.14執筆)
続いて3次のベジェ曲線です。前回の2次曲線は放物線を現している、移動する物体の軌道に良さそうな感じしますが、現物の地形とか凹凸の形状にはちょっと違和感あるかな?
そこで3次曲線を用いたら、地形や自然界の形状にすんなり馴染めるような気がしました。自然界の円、伸縮の形。3次ベジェ曲線。これが地形の下絵にちょうどよかろう。よって、実際に衝突判定で扱うのは3次曲線の壁となります。
れっつとらい♪ヽ(。◕ v ◕。)ノ~*:・'゚☆
3次ベジェ曲線と矩形との当たり判定の手順
衝突判定について、交点を3次方程式の解で求められるけど、計算処理が非常に重たくなるような気もしてます。
そこで単純計算でも判定が取れるように、aabbで判定を取りながら、曲線を分割していく手法を探り当てました。
- 3次ベジェ曲線の、上下左右の極値を求め、AABB矩形を作る
- AABB矩形と衝突相手の矩形で、当たり判定。falseならfalse。或いは、もし始点か終点が矩形と重なれば当たり!
- もしAABB矩形で一旦trueが返ったなら、その地点の3次ベジェ曲線を2つに分割する。分割したそれぞれの端点でAABB矩形を作り、衝突相手の矩形と判定
- trueの返ったAABB矩形からさらに分割...分割した2つのAABB矩形で両方false判定か、端点でtrueが返るまでの繰り返し
3次曲線について、その曲線に接するAABB矩形を求める所がベースになりそうな感じです。 まぁひとまず、3次ベジェ曲線のColliderクラスを定義することから始めていきます。
3次ベジェ曲線のColliderクラスを定義する
class BezierCurve extends Collider { //当たり判定を3次曲線で扱うクラス。地形を現す曲線。固定されたマップの通行判定に使う予定。
constructor(x, y, x1, y1, x2, y2, x3, y3, tag) {
super('bezierCurve', x, y, tag);
this.x1 = x1; //制御点1のx座標
this.y1 = y1; //制御点1のy座標
this.x2 = x2; //制御点2のx座標
this.y2 = y2; //制御点2のy座標
this.x3 = x3; //終着点のx座標
this.y3 = y3; //終着点のy座標
this.BX3 = this.x3 - this.x + 3*(this.x1 - this.x2); // fx(t) t**3の係数
this.BX2 = this.x2 - 2*this.x1 + this.x; // fx(t) t**2の係数の1/3...使う時は3*BX2として使う。
this.BX1 = this.x1 - this.x; // fx(t) t**1の係数の1/3...使う時は3*BX1として使う。
this.BY3 = this.y3 - this.y + 3*(this.y1 - this.y2); // fy(t) t**3の係数
this.BY2 = this.y2 - 2*this.y1 + this.y; // fy(t) t**2の係数の1/3...使う時は3*BY2として使う。
this.BY1 = this.y1 - this.y; // fy(t) t**1の係数の1/3...使う時は3*BY1として使う。
}
/* 3次ベジェ曲線の方程式(0 <= t <=1) t地点の座標を求める*/
fx(t) { return this.BX3*t*t*t + 3*this.BX2*t*t + 3*this.BX1*t + this.x; }
fy(t) { return this.BY3*t*t*t + 3*this.BY2*t*t + 3*this.BY1*t + this.y; }
/*3次ベジェ曲線の微分式(0 <= t <=1) t地点の傾きを調べる*/
f1x(t) { return 3*(this.BX3*t*t + 2*this.BX2*t + this.BX1);}
f1y(t) { return 3*(this.BY3*t*t + 2*this.BY2*t + this.BY1);}
get top() { // 曲線の上端 = Yの最小値
}
get bottom() { // 曲線の下端 = Yの最大値
}
get left() { // 曲線の左端 = Xの最小値
}
get right() { // 曲線の右端 = Xの最大値
}
get aabbRect() { // 曲線と接するaabb矩形
return new Rectangle( this.left, this.top, this.right - this.left, this.bottom - this.top);
}
}
2次曲線のColliderクラスを描いた経験から、3次ベジェ曲線のベースを記述してみました。
なお、始点(x,y),制御点1(x1,y1),制御点2(x2,y2),終点(x3,y3)で定める3次ベジェ曲線の数式を(0 <= t <=1)となる定数tで表すと、こんな感じです。
曲線上のX座標 = fx(t) = (x3 - x + 3*(x1 - x2))*t*t*t + 3*(x2 - 2*x1 + x)*t*t + 3*(x1 - x)*t + x; 曲線上のY座標 = fy(t) = (y3 - y + 3*(y1 - y2))*t*t*t + 3*(y2 - 2*y1 + y)*t*t + 3*(y1 - y)*t + y;
tによる3次方程式になります。案の定長いですね...
で、2乗だったり3乗だったりするそれぞれのtの係数を、曲線の計算式では色んな場面で使います。予め各々の係数を定義しておくと、後の表記も計算も簡略化できて良い感じです。
この係数...前回の2次曲線と比較すると面白い感じです。
tの係数をオブジェクト要素に格納しておく
this.BX3 = this.x3 - this.x + 3*(this.x1 - this.x2); // fx(t) t**3の係数
this.BX2 = this.x2 - 2*this.x1 + this.x; // fx(t) t**2の係数の1/3...使う時は3*BX2として使う。
this.BX1 = this.x1 - this.x; // fx(t) t**1の係数の1/3...使う時は3*BX1として使う。
this.BY3 = this.y3 - this.y + 3*(this.y1 - this.y2); // fy(t) t**3の係数
this.BY2 = this.y2 - 2*this.y1 + this.y; // fy(t) t**2の係数の1/3...使う時は3*BY2として使う。
this.BY1 = this.y1 - this.y; // fy(t) t**1の係数の1/3...使う時は3*BY1として使う。
すると曲線上のX,Y座標を求めるfx(t)、fy(t)の式が、簡潔に表現できるようになります。
/* 3次ベジェ曲線の方程式(0 <= t <=1) t地点の座標を求める*/
fx(t) { return this.BX3*t*t*t + 3*this.BX2*t*t + 3*this.BX1*t + this.x; }
fy(t) { return this.BY3*t*t*t + 3*this.BY2*t*t + 3*this.BY1*t + this.y; }
あとは微分式ですね。微分式は、その地点での曲線の傾き具合を求めることが出来ます。この計算式を用いて、XやYの座標が極値となるtのタイミングを求めたりできるし、衝突判定で法線ベクトルを求めたりするのにも使います。
/* 3次ベジェ曲線の微分式(0 <= t <=1) t地点の傾きを求める*/
f1x(t) { return 3*(this.BX3*t*t + 2*this.BX2*t + this.BX1); }
f1y(t) { return 3*(this.BY3*t*t + 2*this.BY2*t + this.BY1); }
3次ベジェ曲線のAABB矩形を求める
3次曲線クラスの基盤ができました。ここから、曲線の上下左右の端となるX,Y座標を求めて、AABB矩形を作っていきたいと思います。
イメージとしてはこんな感じです。
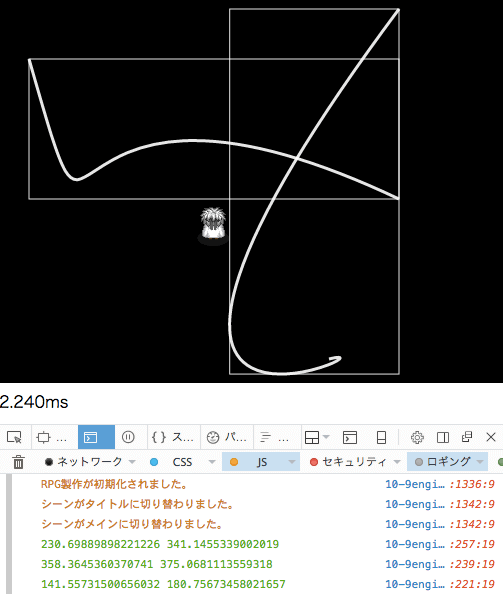
ではでは2次曲線のときと同じように、上端の座標(Yの最小値)を求める所からやっていこうと思います。
曲線上のYの最小値(上端)を求める式
get top() { // 曲線の上端 = Yの最小値
if( Math.min(this.y, this.y1, this.y2, this.y3) == Math.min(this.y, this.y3) ) { //もし最小値が始点か終点なら
return Math.min(this.y, this.y3); //始点か終点のうち、どちらか小さい方が最小値。
}
else { //もし最小値が制御点となるなら、Yの極値を比べる
const t1,t2 = f1y(t) = 0 となるようなtの値。2次方程式なので2つある可能性
const yLim1 = fy(t1), yLim2 = fy(t2); // 極値は、微分式の解(t)を元の式に代入して求める
return Math.min(this.y, this.y3, yLim1, yLim2); //始点、終点、いずれかの極値が最小値。
}
}
大体こんなノリではなかろうか(。0 _ 0。)ノ
- まず始点か終点が、最小値にあてはまるならそこで計算は終了する
- もし制御点が最小値になるなら、yの傾きが0となる極値のt地点を求めて、そのtを元の関数に代入してy座標の極値を得る
- 得られた極値と始点、終点それぞれで最終比較して、一番小さな値が上端!
微分方程式の解は2次...極値となるtが2つ出てくる。。。どうにも計算の複雑な部分は日本語で描きました。日本語すばらしい!
でも、これだとプログラムが動かないので、プログラム言語に書き換えなければなりません。書き換えます(o _ o。)
yの微分式=0となるtを求める
f1y(t) = 3*(this.BY3*t*t + 2*this.BY2*t + this.BY1) = 0;となるtの値
この微分式の解は、2次方程式なので解の公式が使えます。
しかも、1次の係数が2の倍数になってるので、より簡略化した解の式が得られます。
これによって極値となるtの値が2つ求まります。
const t1 = - this.BY2 + Math.sqrt(this.BY2*this.BY2 + this.BY3*this.BY1) / this.BY3; const t2 = - this.BY2 - Math.sqrt(this.BY2*this.BY2 + this.BY3*this.BY1) / this.BY3;
Yの極値を求める(二つある)
あとはこのtをY座標を求める関数に代入して、Yの極値となる2つの値を求めます。const yLim1 = this.fy(t1); //Yの極値その1 const yLim2 = this.fy(t2); //Yの極値その2
求めた2つの極値と、始点、終点で比較
最後に、求めた2つの極値と始点、終点を比較して、最も最小となる値が、上端のY座標となります。return Math.min(this.y, this.y2, this.yLim1, this.yLim2); //始点、終点、いずれかの極値が最小値。
まとめ
ここまでのコードをまとめると、上端のY座標を求める関数はこんな感じです。
get top() { // 曲線の上端 = Yの最小値
if( Math.min(this.y, this.y1, this.y2, this.y3) == Math.min(this.y, this.y3) ) { //もし最小値が始点か終点なら
return Math.min(this.y, this.y3); //始点か終点のうち、どちらか小さい方が最小値。
}
else { //もし最小値が制御点となるなら、Yの極値を比べる
const t1 = - this.BY2 + Math.sqrt(this.BY2*this.BY2 + this.BY3*this.BY1) / this.BY3;
const t2 = - this.BY2 - Math.sqrt(this.BY2*this.BY2 + this.BY3*this.BY1) / this.BY3;
const yLim1 = this.fy(t1); //Yの極値その1
const yLim2 = this.fy(t2); //Yの極値その2
return Math.min(this.y, this.y3, yLim1, yLim2); //いずれかの極値が最小値。
}
}
まぁこんな要領で、下端の場合はYの最大値を求める。
左端はXの最小値を求め、右端はXの最大値を求める。
というのをすると、四隅となる点が求まるので、それらの点を使って矩形を描けるようになるでしょう。
試しに、3次ベジェ曲線のアクタークラスにAABB矩形を描画させるコードを追加して、デモを確認するか。
3次曲線のアクタークラスにAABB矩形を描画させるコード
class BezierCurveActor extends Actor { //3次ベジェ曲線
constructor(x, y, x1, y1, x2, y2, x3, y3, tag, isFall=false) {
const hitArea = new BezierCurve(x, y, x1, y1, x2, y2, x3, y3, tag);
super(x, y, hitArea, ['object']);
this.x1 = x1; //制御点1のx座標
this.y1 = y1; //制御点1のy座標
this.x2 = x2; //制御点2のx座標
this.y2 = y2; //制御点2のy座標
this.x3 = x3; //終着点のx座標
this.y3 = y3; //終着点のy座標
this.isFall = isFall; //一方通行にするかどうか
this._color = 'rgba(255, 255, 255, 0.9)'; //線画の色指定
this.addEventListener('hit', (e) => this._color = 'rgba(255, 0, 0, 0.9)' ); //当たり判定の時に赤くする
}
get x() { return this._x; } set x(value) { this._x = value; }//x座標に値を代入する関数をActorから上書き
get y() { return this._y; } set y(value) { this._y = value; }//y座標に値を代入する関数をActorから上書き
update(gameInfo, input) {
this._color = 'rgba(255, 255, 255, 0.9)';
}
render(target, scroller) {
const context = target.getContext('2d');
context.strokeStyle = this._color;
context.lineWidth = 3;
context.beginPath(); //描画位置の初期化
context.moveTo(this.x + scroller.x, this.y + scroller.y); //曲線のスタート位置を指定
context.bezierCurveTo(this.x1 + scroller.x, this.y1 + scroller.y,
this.x2 + scroller.x, this.y2 + scroller.y,
this.x3 + scroller.x, this.y3 + scroller.y); //制御点1、制御点2、終着点をそれぞれ指定して曲線の軌道を描く
context.stroke(); //軌道に沿って線を引く
context.lineWidth = 1;
context.beginPath(); //ここからaabb矩形も可視化してみる。
context.strokeRect(this.hitArea.left, this.hitArea.top, this.hitArea.aabbRect.width, this.hitArea.aabbRect.height);
}
}
アクタークラスはこんなもん(' '*)...
ではデモを見てみます。
??????!!!!
どういうことだってば??
片方の曲線は問題なく表示されてるのに、もう片方には表示されてません。。
なぜだ、同じ曲線クラスから作ってるので、同様に矩形ができないとおかしい筈なんですけどね。
ちなみにシーンに追加した(矩形が表示されない方の)曲線の座標はこんな感じ。
class MainScene extends Scene {
constructor(renderingTarget) {
super('メイン', 1800, 1600, 'black', renderingTarget);
const npc = new NPC(150, 100);
this.add(npc);
this.add(global.player);
const Curve2 = new BezierCurveActor (30, 60, 110, 340, 20, 20, 400, 200, 'wall');
this.add(Curve2);
}
}
new BezierCurveActor (30, 60, 110, 340, 20, 20, 400, 200, 'wall');
。。。制御点2が、始点のx座標よりも小さな値になると、表示されなくなってしまいました。
これを例えばnew BezierCurveActor (30, 60, 110, 340, 30, 20, 400, 200, 'wall');
とかにして、始点のX座標より小さくならないようにすると、問題なく表示されます。
検証として、aabb矩形を取り出すときに(x,y,width,height)の値がどうなってるかも確認してみますか...
aabb矩形のget()関数に検証用のconsole.logを追加
get aabbRect() { // 曲線と接するaabb矩形
console.log(this.left, this.top, this.right - this.left, this.bottom - this.top); //ここを追加
return new Rectangle( this.left, this.top, this.right - this.left, this.bottom - this.top);
}
こちらが表示された時のAABB矩形4隅の座標。
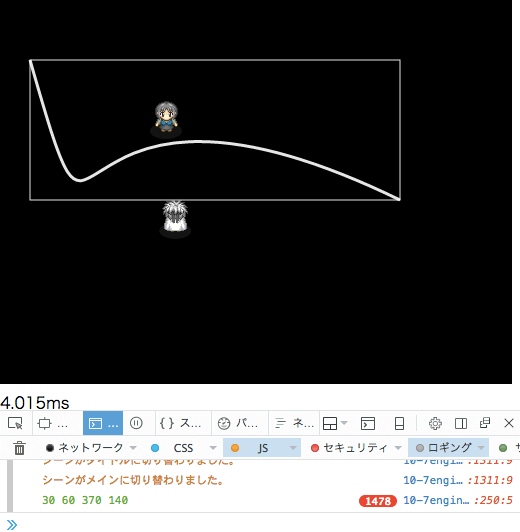
こちらが表示されない場合のAABB矩形4隅の座標。
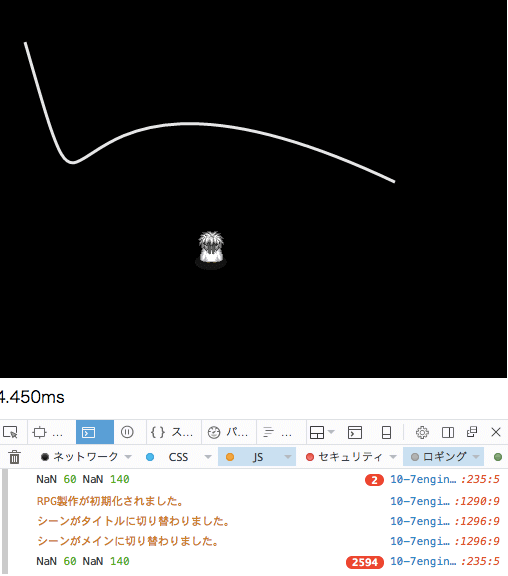
表示されない時、座標値がNaNで吐き出されている。。。。(o _ o。)
NaNというのは「計算不可能」な値ということだそうです。
これ、ちょい心当たり有りまして、微分式で求めたtの解が存在しない場合です。
もしtの解が存在しないなら、極値も存在しない。のに関わらず、存在しない値をMath.min()関数に入れ込んでしまった。
すると、存在しない値から吐き出される計算結果は、すべてNaNとして評価されてしまう。
よって、4隅を求める関数を使った矩形の座標も、存在しなくなってしまうのです!!! 失敗。
この辺の、tが虚数解の場合を考慮して、元(Collider側)の関数計算を組み直す必要がありそうです。
fx(t),fy(t)のtが存在しない場合を考慮した計算方法
/* 3次ベジェ曲線の方程式(0 <= t <=1) t地点の座標を求める*/
fx(t) { return t > 0 ? this.BX3*t*t*t + this.BX2*t*t + this.BX1*t + this.x : this.x; } //tが実数なら、t値を代入してX座標を取得。それ以外ならt=0を代入
fy(t) { return t > 0 ? this.BY3*t*t*t + this.BY2*t*t + this.BY1*t + this.y : this.y; } //tが実数なら、t値を代入してY座標を取得。それ以外ならt=0を代入
座標を求める関数に、代入するtが実数なら。。。という条件を追加します。
これがエラー対処法の1つの解答になるでしょう。
もう一つ、そもそも微分式 = 0のtが存在しない場合のプログラム計算も考えてみます。
その場合は極値が存在しないことになるので、元の始点か終点のうちどちらかを選ぶことになります。
微分式=0の解が存在しない場合、始点か終点で選ぶ
get top() { // 曲線の上端 = Yの最小値
if( Math.min(this.y, this.y1, this.y2, this.y3) == Math.min(this.y, this.y3) ) { //もし最小値が始点か終点なら
return Math.min(this.y, this.y3); //始点か終点のうち、どちらか小さい方が最小値。
}
else { //もし最小値が制御点となるなら、Yの極値を比べる
const delta = this.BY2*this.BY2 + this.BY3*this.BY1; // Math.sqrtの中身でまず判定
if( delta < 0 ) { return Math.min(this.y, this.y3); } // 解が存在しないなら、始点か終点で判定
const sqrtDelta = Math.sqrt(delta); // ルート計算を保持しておく
const t1 = - this.BY2 + sqrtDelta / this.BY3;
const t2 = - this.BY2 - sqrtDelta / this.BY3;
const yLim1 = this.fy(t1); //Yの極値その1
const yLim2 = this.fy(t2); //Yの極値その2
return Math.min(this.y, this.y3, yLim1, yLim2); //いずれかの極値が最小値。
}
}
プログラムで表現すると、こんな感じになるでしょう。
これでAABB矩形が問題なく表示されるはずです。
get top()〜の関数を高速化する
このコードは、もう一点問題が有りました。ログを見たら分かる通り、get top()、bottom()、left()、right()、で該当箇所が1秒毎に2次方程式を何度も計算してしまってます。毎秒60回ずつ... お陰で曲線一つに4msもの時間(上限は15msくらい)を消費してしまってるのです。。。。コレは重すぎてやばいですね。
なので、計算結果を要素に格納できるようにして、2回め以降はすぐに取り出せるよう改良を加えたいと思います。
これがキャッシュの概念だろうか??(' '*) 判らないけど、計算で得られた数字を保存しとくみたいな。
一度計算したら値を保存できるように書き換え
get top() { // 曲線の上端 = Yの最小値
if(this.yMin === null) { //まだYの最小値が定まってないなら計算する
if( Math.min(this.y, this.y1, this.y2, this.y3) == Math.min(this.y, this.y3) ) { //もし最小値が始点か終点なら
this.yMin = Math.min(this.y, this.y3); //始点か終点のうち、どちらか小さい方が最小値
}
else { //もし最小値が制御点となるなら、Yの極値を比べる
const delta = this.BY2*this.BY2 - this.BY3*this.BY1;
if( delta < 0 ) {//微分式=0のtが虚数解になるなら
this.yMin = Math.min(this.y, this.y3); // 最小値最大値は、始点と終点の値で求める
} else { const sqrtDelta = Math.sqrt(delta); // もし微分式の解が存在するなら2つの極値が求まる
const yLim1 = this.fy( (-this.BY2 + sqrtDelta)/this.BY3 );
const yLim2 = this.fy( (-this.BY2 - sqrtDelta)/this.BY3 );
this.yMin = Math.min(this.y, this.y3, yLim1, yLim2); //いずれかの値が最小値。
}
}
}
return this.yMin;
}
曲線の要素に、this.yMinというのを追加しました。
もし値が空なら、yの最小値を計算してthis.yTopに値を格納します。
そして、this.yMinをreturnする。すると2回め以降、this.yMinをreturnするだけで上端のy座標が得られるので、AABB矩形を描くのに大幅な短縮効果がでてくるです。
表示速度、大分高速化されたのではなかろうか(' '*)

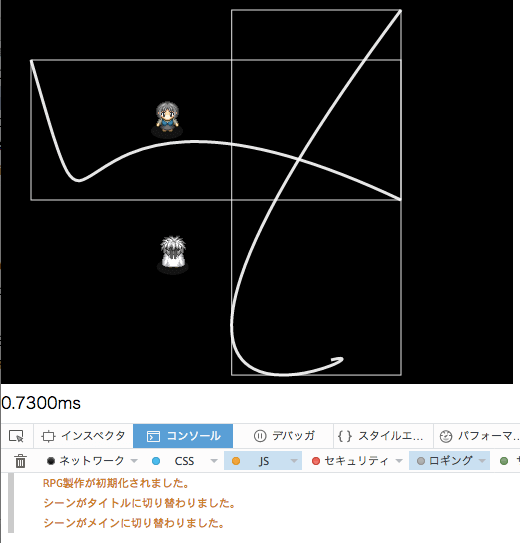
ここまでの3次曲線(Collider)クラスのまとめ
class BezierCurve extends Collider { //当たり判定を3次曲線で扱うクラス。地形を現す曲線。固定されたマップの通行判定に使う予定。
constructor(x, y, x1, y1, x2, y2, x3, y3, tag) {
super('bezierCurve', x, y, tag);
this.x1 = x1; //制御点1のx座標
this.y1 = y1; //制御点1のy座標
this.x2 = x2; //制御点2のx座標
this.y2 = y2; //制御点2のy座標
this.x3 = x3; //終着点のx座標
this.y3 = y3; //終着点のy座標
this.BX3 = this.x3 - this.x + 3*(this.x1 - this.x2); // fx(t) t**3の係数
this.BX2 = this.x2 - 2*this.x1 + this.x; // fx(t) t**2の係数の1/3...使う時は3*BX2として使う。
this.BX1 = this.x1 - this.x; // fx(t) t**1の係数の1/3...使う時は3*BX1として使う。
this.BY3 = this.y3 - this.y + 3*(this.y1 - this.y2); // fy(t) t**3の係数
this.BY2 = this.y2 - 2*this.y1 + this.y; // fy(t) t**2の係数の1/3...使う時は3*BY2として使う。
this.BY1 = this.y1 - this.y; // fy(t) t**1の係数の1/3...使う時は3*BY1として使う。
// 曲線のAABB矩形を囲む4隅の座標を保存する要素
this.yMin = null;
this.yMax = null;
this.xMin = null;
this.xMax = null;
}
/* 3次ベジェ曲線の方程式(0 <= t <=1) t地点の座標を求める*/
fx(t) { return t > 0 ? this.BX3*t*t*t + 3*this.BX2*t*t + 3*this.BX1*t + this.x : this.x; } //tが実数なら、tを代入してX座標取得。それ以外ならt=0を代入
fy(t) { return t > 0 ? this.BY3*t*t*t + 3*this.BY2*t*t + 3*this.BY1*t + this.y : this.y; } //tが実数なら、tを代入してY座標取得。それ以外ならt=0を代入
/*3次ベジェ曲線の微分式(0 <= t <=1) t地点の傾きを調べる*/
f1x(t) { return 3*(this.BX3*t*t + 2*this.BX2*t + this.BX1);}
f1y(t) { return 3*(this.BY3*t*t + 2*this.BY2*t + this.BY1);}
get top() { // 曲線の上端 = Yの最小値
if(this.yMin === null) { //まだYの最小値が定まってないなら計算する
if( Math.min(this.y, this.y1, this.y2, this.y3) == Math.min(this.y, this.y3) ) { //もし最小値が始点か終点なら
this.yMin = Math.min(this.y, this.y3); //始点か終点のうち、どちらか小さい方が最小値
}
else { //もし最小値が制御点となるなら、Yの極値を比べる
const delta = this.BY2*this.BY2 - this.BY3*this.BY1;
if( delta < 0 ) {//微分式=0のtが虚数解になるなら
this.yMin = Math.min(this.y, this.y3); // 最小値最大値は、始点と終点の値で求める
} else { const sqrtDelta = Math.sqrt(delta); // もし微分式の解が存在するなら2つの極値が求まる
const yLim1 = this.fy( (-this.BY2 + sqrtDelta)/this.BY3 );
const yLim2 = this.fy( (-this.BY2 - sqrtDelta)/this.BY3 );
this.yMin = Math.min(this.y, this.y3, yLim1, yLim2); //いずれかの値が最小値。
}
}
}
return this.yMin;
}
get bottom() { // 曲線の下端 = Yの最大値
if(this.yMax === null) { //まだYの最大値が定まってないなら計算する
if( Math.max(this.y, this.y1, this.y2, this.y3) == Math.max(this.y, this.y3) ) { //もし最大値が始点か終点なら
this.yMax = Math.max(this.y, this.y3); //始点か終点のうち、どちらか大きい方が最大値。
}
else { //もし最小値が制御点となるなら、Yの極値を比べる
const delta = this.BY2*this.BY2 - this.BY3*this.BY1;
if( delta < 0 ) {//微分式=0のtが虚数解になるなら
this.yMax = Math.max(this.y, this.y3); // 最小値最大値は、始点と終点の値で求める
} else { const sqrtDelta = Math.sqrt(delta); // もし微分式の解が存在するなら2つの極値が求まる
const yLim1 = this.fy( (-this.BY2 + sqrtDelta)/this.BY3 );
const yLim2 = this.fy( (-this.BY2 - sqrtDelta)/this.BY3 );
this.yMax = Math.max(this.y, this.y3, yLim1, yLim2); //いずれかの値が最大値
}
}
}
return this.yMax;
}
get left() { // 曲線の左端 = Xの最小値
if(this.xMin === null) { //まだXの最小値が定まってないなら計算する
if( Math.min(this.x, this.x1, this.x2, this.x3) == Math.min(this.x, this.x3) ) { //もし最小値が始点か終点なら
this.xMin = Math.min(this.x, this.x3); //始点か終点のうち、どちらか小さい方が最小値
}
else { //もし最小値が制御点となるなら、Xの極値を比べる
const delta = this.BX2*this.BX2 - this.BX3*this.BX1;
if( delta < 0 ) {//微分式=0のtが虚数解になるなら
this.xMin = Math.min(this.x, this.x3); // 最小値最大値は、始点と終点の値で求める
} else { const sqrtDelta = Math.sqrt(delta); // もし微分式の解が存在するなら2つの極値が求まる
const xLim1 = this.fx( (-this.BX2 + sqrtDelta)/this.BX3 );
const xLim2 = this.fx( (-this.BX2 - sqrtDelta)/this.BX3 );
this.xMin = Math.min(this.x, this.x3, xLim1, xLim2); //いずれかの値が最小値
}
}
}
return this.xMin;
}
get right() { // 曲線の右端 = Xの最大値
if(this.xMax === null) { //まだXの最大値が定まってないなら計算する
if( Math.max(this.x, this.x1, this.x2, this.x3) == Math.max(this.x, this.x3) ) { //もし最大値が始点か終点なら
this.xMax = Math.max(this.x, this.x3); //始点か終点のうち、どちらか大きい方が最大値
}
else { //もし最小値が制御点となるなら、Xの極値を比べる
const delta = this.BX2*this.BX2 - this.BX3*this.BX1;
if( delta < 0 ) {//微分式=0のtが虚数解になるなら
this.xMax = Math.max(this.x, this.x3); // 最小値最大値は、始点と終点の値で求める
} else { const sqrtDelta = Math.sqrt(delta); // もし微分式の解が存在するなら2つの極値が求まる
const xLim1 = this.fx( (-this.BX2 + sqrtDelta)/this.BX3 );
const xLim2 = this.fx( (-this.BX2 - sqrtDelta)/this.BX3 );
this.xMax = Math.max(this.x, this.x3, xLim1, xLim2); //いずれかの値が最大値
}
}
}
return this.xMax;
}
get aabbRect() { // 曲線と接するaabb矩形
return new Rectangle( this.left, this.top, this.right - this.left, this.bottom - this.top);
}
}
0 <=t<= 0.5, 0.5 <=t<= 1, 3次曲線を2分割したAABB矩形を求めたい
では続いて、3次曲線をちょうど半分に分割した区間で、2つのAABB矩形を作りたいと思います。
全体のAABB曲線で求めたX,Yの極値とtの値が、ここでも必要になりそうですね。
おそらく当たり判定時に使い回すだろう、極値を求める関数に改良を加えて、予めthis.の要素内に格納しておきたいと思います。
Yの極値となるtの値を配列で求める
tLimYcheck() { // Yの極値となるt値を求める
const delta = this.BY2*this.BY2 - this.BY3*this.BY1;
if( delta <= 0 ) { return; }//微分式=0のtが虚数解になるならYの極値tは無い
else { const sqrtDelta = Math.sqrt(delta); // 解の公式より、2つの解が求まる。
const tCheck = []; // 求めたtの解が0〜1の間のみ条件を満たす
tCheck.push( (-this.BY2 + sqrtDelta)/this.BY3 );
tCheck.push( (-this.BY2 - sqrtDelta)/this.BY3 );
for(let t of tCheck) {
if(0 < t && t < 1) {this.tLimY.push(t); }
}
this.tLimY.sort( (a,c) => a-c ); // tの配列を昇順に
console.log(this.tLimY);
}
}
fy(t)の微分式より、f1y(t)=0となるようなtの解を、2次方程式の解の公式Ⅱを用いて解きます。
もし解が一つの場合は、傾きの符号変化がないので極値とは捉えません。解が二つ出る場合に、その地点をY座標の極値(凸か凹)として捉えます。
求めた解を検証し、0 < t < 1を満たす場合のみ配列に追加し、昇順にソートしてthis.tLimYという要素に格納する。といった手順です。
これをX座標についても同様に行い、constructor内にてこの関数を呼び出します(この関数は、newされたときに1回だけ呼び出される)
3次曲線クラスのconstructor内に追記
class BezierCurve extends Collider { //当たり判定を3次曲線で扱うクラス。地形を現す曲線なのでマップに固定。通行判定に使う予定。
constructor(x, y, x1, y1, x2, y2, x3, y3, tag) {
super('bezierCurve', x, y, tag);
this.x1 = x1; //制御点1のx座標
this.y1 = y1; //制御点1のy座標
this.x2 = x2; //制御点2のx座標
this.y2 = y2; //制御点2のy座標
this.x3 = x3; //終着点のx座標
this.y3 = y3; //終着点のy座標
this.BX3 = this.x3 - this.x + 3*(this.x1 - this.x2); // fx(t) t**3の係数
this.BX2 = this.x2 - 2*this.x1 + this.x; // fx(t) t**2の係数の1/3...使う時は3*BX2として使う。
this.BX1 = this.x1 - this.x; // fx(t) t**1の係数の1/3...使う時は3*BX1として使う。
this.BY3 = this.y3 - this.y + 3*(this.y1 - this.y2); // fy(t) t**3の係数
this.BY2 = this.y2 - 2*this.y1 + this.y; // fy(t) t**2の係数の1/3...使う時は3*BY2として使う。
this.BY1 = this.y1 - this.y; // fy(t) t**1の係数の1/3...使う時は3*BY1として使う。
// X,Yそれぞれが極値となるtの値。最大で2つずつ存在
this.tLimX = [];
this.tLimY = [];
// X,Yの極値となるt値を求める
this.tLimXcheck();
this.tLimYcheck();
// 求めたtの配列から、X,Yの極値の座標を配列に格納する
this.limX = this.tLimX.map( (t) => this.fx(t) )
this.limY = this.tLimY.map( (t) => this.fy(t) )
// 曲線のAABB矩形を囲む4隅の座標を保存する要素
this.yMin = null;
this.yMax = null;
this.xMin = null;
this.xMax = null;
}
/* 3次ベジェ曲線の方程式(0 <= t <=1) t地点の座標を求める*/
fx(t) { return this.BX3*t*t*t + 3*this.BX2*t*t + 3*this.BX1*t + this.x; } //tを代入してX座標取得。
fy(t) { return this.BY3*t*t*t + 3*this.BY2*t*t + 3*this.BY1*t + this.y; } //tを代入してY座標取得。
/*3次ベジェ曲線の微分式(0 <= t <=1) t地点の傾きを調べる*/
f1x(t) { return 3*(this.BX3*t*t + 2*this.BX2*t + this.BX1);}
f1y(t) { return 3*(this.BY3*t*t + 2*this.BY2*t + this.BY1);}
tLimXcheck() { // Xの極値となるt値を求める
const delta = this.BX2*this.BX2 - this.BX3*this.BX1;
if( delta <= 0 ) { return; }//微分式=0のtが虚数解になるならYの極値tは無い
else { const sqrtDelta = Math.sqrt(delta); // 解の公式より、2つの解が求まる。
const tCheck = []; // 求めたtの解が0〜1の間のみ条件を満たす
tCheck.push( (-this.BX2 + sqrtDelta)/this.BX3 );
tCheck.push( (-this.BX2 - sqrtDelta)/this.BX3 );
for(let t of tCheck) {
if(0 < t && t < 1) { this.tLimX.push(t); }
}
this.tLimX.sort( (a,c) => a-c ); // tの配列を昇順に
console.log(this.tLimX);
}
}
tLimYcheck() { // Yの極値となるt値を求める
const delta = this.BY2*this.BY2 - this.BY3*this.BY1;
if( delta <= 0 ) { return; }//微分式=0のtが虚数解になるならYの極値tは無い
else { const sqrtDelta = Math.sqrt(delta); // 解の公式より、2つの解が求まる。
const tCheck = []; // 求めたtの解が0〜1の間のみ条件を満たす
tCheck.push( (-this.BY2 + sqrtDelta)/this.BY3 );
tCheck.push( (-this.BY2 - sqrtDelta)/this.BY3 );
for(let t of tCheck) {
if(0 < t && t < 1) {this.tLimY.push(t); }
}
this.tLimY.sort( (a,c) => a-c ); // tの配列を昇順に
console.log(this.tLimY);
}
}
次に求めた極値となるtから、配列のメソッド.mapを使って、fx(t),fy(t)にそれぞれ代入した座標を、新しい配列で取得します。
// 求めたtの配列から、X,Yの極値の座標を配列に格納する
this.limX = this.tLimX.map( (t) => this.fx(t) )
this.limY = this.tLimY.map( (t) => this.fy(t) )
下準備としてはこんなものか。
すると、前回の項で描いたaabb矩形の4隅を求める関数がかなり簡略化されました。
get top()の関数修正後
get top() { // 曲線の上端 = Yの最小値
if(this.yMin === null) { //まだYの最小値が定まってないなら計算する
this.yMin = Math.min(this.y, this.y3, ...this.limY); //いずれかの値が最小値。
console.log(this.y, this.y3, ...this.limY);
}
return this.yMin;
}
console.logで値を取得してみますと、コードがきちんと稼働してるか確認をとれます。
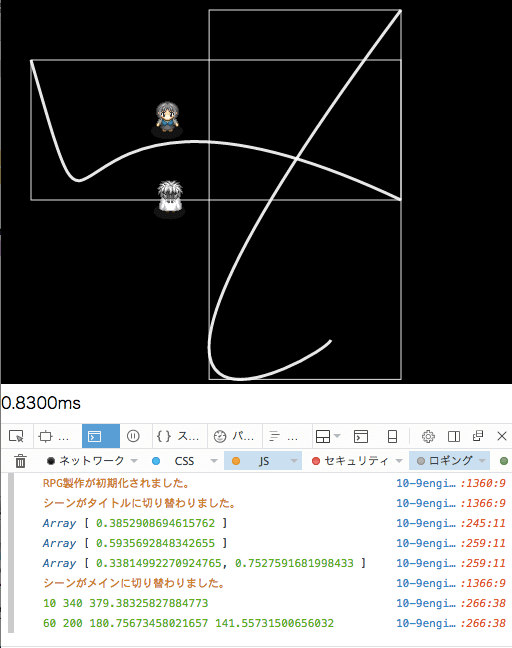
区間内のYの最小値を求めるyMin()を定義する
さて、後は区間を分割した時に、その区間内における新しい4隅を計算できたら良いですね。
...
もしかすると、this.yMinとthis.topは、名前と機能を逆にした方がいいかな... this.topは他の形状にも使いまわしてる凡庸の定義です。これから区間を絞って新しいtopを求めるとするなら、その関数はyMinに割り当てたほうが良い。 で、this.topの値はtが0〜1の全体範囲で取得したyMin(Yの最小値の座標)とすれば、いい感じに整理できそうですよ。試しに作ってみます。
yMin(t0, t1) { /* tがt0〜t1における範囲の、yの最小値を求める(初期値は0 <= t <=1 */
const yCheck = [this.fy(t0), this.fy(t1)]; // まず両端のy座標をチェックリストに追加
for (let i=0; i < this.tLimY.length; i++) { // 極値となるtが範囲内か順番に確認
if( t1 <= this.tLimY[i] ) { return Math.min(...yCheck); } // 昇順なので、すでに大きい場合はこの時点で結果をreturnできる
if( t0 < this.tLimY[i] ) { yCheck.push(this.limY[i]); } // もし極値となるtが範囲内なら、極値の座標もチェックリストに加える
}
console.log(yCheck);
return Math.min(...yCheck); // 範囲内のyの最小値を返す
}
で、constructor内にてtopだけこの関数に置き換えてみました。てすとてすとです。
// 曲線のAABB矩形を囲む4隅の座標を保存する要素
this.top = this.yMin(0, 1); //tが0〜1の間のyの最小値が上端
this.yMax = null;
this.xMin = null;
this.xMax = null;
}
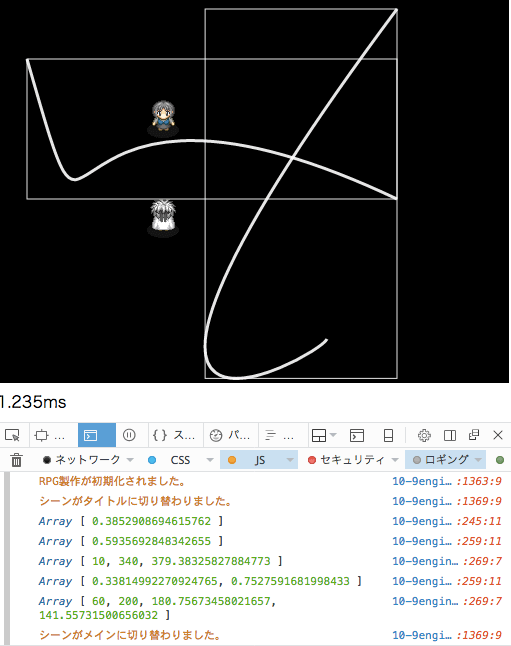
いい感じに表示されました。よってaabb矩形の4隅ともこのような関数に置き換えてOKになりました。
4隅の計算を書き換えて、全体のコードをもう一度掲載します。だいぶ答えに近づいてきました。
さらに改良後の3次曲線(Collider)クラス
class BezierCurve extends Collider { //当たり判定を3次曲線で扱うクラス。地形を現す曲線なのでマップに固定。通行判定に使う予定。
constructor(x, y, x1, y1, x2, y2, x3, y3, tag) {
super('bezierCurve', x, y, tag);
this.x1 = x1; //制御点1のx座標
this.y1 = y1; //制御点1のy座標
this.x2 = x2; //制御点2のx座標
this.y2 = y2; //制御点2のy座標
this.x3 = x3; //終着点のx座標
this.y3 = y3; //終着点のy座標
this.BX3 = this.x3 - this.x + 3*(this.x1 - this.x2); // fx(t) t**3の係数
this.BX2 = this.x2 - 2*this.x1 + this.x; // fx(t) t**2の係数の1/3...使う時は3*BX2として使う。
this.BX1 = this.x1 - this.x; // fx(t) t**1の係数の1/3...使う時は3*BX1として使う。
this.BY3 = this.y3 - this.y + 3*(this.y1 - this.y2); // fy(t) t**3の係数
this.BY2 = this.y2 - 2*this.y1 + this.y; // fy(t) t**2の係数の1/3...使う時は3*BY2として使う。
this.BY1 = this.y1 - this.y; // fy(t) t**1の係数の1/3...使う時は3*BY1として使う。
// X,Yそれぞれが極値となるt値を格納。値は最大2つずつ存在
this.xLimT = [];
this.yLimT = [];
// X,Yの極値となるt値を求める
this.xLimTcheck();
this.yLimTcheck();
// 求めたtの配列から、X,Yの極値の座標を配列に格納する
this.XnoKIWAMI = this.xLimT.map( (t) => this.fx(t) )
this.YnoKIWAMI = this.yLimT.map( (t) => this.fy(t) )
const yMinMax = this.yMinMax(0, 1);
const xMinMax = this.xMinMax(0, 1);
// 曲線のAABB矩形を囲む4隅の座標を保存する要素
this.top = yMinMax.min; //tが0〜1の間のyの最小値が上端
this.bottom = yMinMax.max; //tが0〜1の間のyの最大値が下端
this.left = xMinMax.min; //tが0〜1の間のxの最小値が左端
this.right = xMinMax.max; //tが0〜1の間のxの最大値が右端
}
/* 3次ベジェ曲線の方程式(0 <= t <=1) t地点の座標を求める*/
fx(t) { return this.BX3*t*t*t + 3*this.BX2*t*t + 3*this.BX1*t + this.x; } //tを代入してX座標取得。
fy(t) { return this.BY3*t*t*t + 3*this.BY2*t*t + 3*this.BY1*t + this.y; } //tを代入してY座標取得。
/*3次ベジェ曲線の微分式(0 <= t <=1) t地点の傾きを調べる*/
f1x(t) { return 3*(this.BX3*t*t + 2*this.BX2*t + this.BX1);}
f1y(t) { return 3*(this.BY3*t*t + 2*this.BY2*t + this.BY1);}
xLimTcheck() { // Xの極値となるt値を求める
const delta = this.BX2*this.BX2 - this.BX3*this.BX1;
if( delta <= 0 ) { return; }//微分式=0のtが虚数解になるならYの極値tは無い
else { const sqrtDelta = Math.sqrt(delta); // 解の公式より、2つの解が求まる。
const tCheck = []; // 求めたtの解が0〜1の間のみ条件を満たす
tCheck.push( (-this.BX2 + sqrtDelta)/this.BX3 );
tCheck.push( (-this.BX2 - sqrtDelta)/this.BX3 );
for(let t of tCheck) {
if(0 < t && t < 1) { this.xLimT.push(t); }
}
this.xLimT.sort( (a,c) => a-c ); // tの配列を昇順に
console.log(this.xLimT);
}
}
yLimTcheck() { // Yの極値となるt値を求める
const delta = this.BY2*this.BY2 - this.BY3*this.BY1;
if( delta <= 0 ) { return; }//微分式=0のtが虚数解になるならYの極値tは無い
else { const sqrtDelta = Math.sqrt(delta); // 解の公式より、2つの解が求まる。
const tCheck = []; // 求めたtの解が0〜1の間のみ条件を満たす
tCheck.push( (-this.BY2 + sqrtDelta)/this.BY3 );
tCheck.push( (-this.BY2 - sqrtDelta)/this.BY3 );
for(let t of tCheck) {
if(0 < t && t < 1) {this.yLimT.push(t); }
}
this.yLimT.sort( (a,c) => a-c ); // tの配列を昇順に
console.log(this.yLimT);
}
}
yMinMax(t0, t1) { /* tがt0〜t1における範囲の、yの最大最小を求める(初期値は0 <= t <=1 */
const yCheck = [this.fy(t0), this.fy(t1)]; // まず両端のy座標をチェックリストに追加
for (let i=0; i < this.yLimT.length; i++) { // 極値となるtが範囲内か順番に確認
if( t1 <= this.yLimT[i] ) { return { min:Math.min(...yCheck), max:Math.max(...yCheck) }; } // 昇順なので、すでに大きい場合はこの時点で結果をreturnできる
if( t0 < this.yLimT[i] ) { yCheck.push(this.YnoKIWAMI[i]); } // もし極値となるtが範囲内なら、極値の座標もチェックリストに加える
}
return { min:Math.min(...yCheck), max:Math.max(...yCheck) }; // 範囲内のyの最小値と最大値を返す
}
xMinMax(t0, t1) { /* tがt0〜t1における範囲の、xの最大最小を求める(初期値は0 <= t <=1 */
const xCheck = [this.fx(t0), this.fx(t1)]; // まず両端のx座標をチェックリストに追加
for (let i=0; i < this.xLimT.length; i++) { // 極値となるtが範囲内か順番に確認
if( t1 <= this.xLimT[i] ) { return { min:Math.min(...xCheck), max:Math.max(...xCheck) }; } // 昇順なので、すでに大きい場合はこの時点で結果をreturnできる
if( t0 < this.xLimT[i] ) { xCheck.push(this.XnoKIWAMI[i]); } // もし極値となるtが範囲内なら、極値の座標もチェックリストに加える
}
return { min:Math.min(...xCheck), max:Math.max(...xCheck) }; // 範囲内のxの最小値と最大値を返す
}
get aabbRect() { // 曲線と接するaabb矩形
return new Rectangle( this.left, this.top, this.right - this.left, this.bottom - this.top);
}
aabbRect2(t0, t1) { //t0〜t1の区間で分割した曲線のaabb矩形
const xLim = this.xMinMax(t0, t1), yLim = this.yMinMax(t0, t1);
const width = xLim.max - xLim.min;
const height = yLim.max - yLim.min;
return new Rectangle( xLim.min, yLim.min, width, height );
}
}
ここまで下準備です(。◕ ∀ ◕。)ノ
でも下準備しっかりすると、計算早くて良さ気です。
そろそろ本題。曲線を2分割にしたaabb矩形を2つ描いてみます。
区間を分割したaabb矩形を求める関数
aabbRect2(t0, t1) { //t0〜t1の区間で分割した曲線のaabb矩形
const xLim = this.xMinMax(t0, t1), yLim = this.yMinMax(t0, t1);
const width = xLim.max - xLim.min;
const height = yLim.max - yLim.min;
return new Rectangle( xLim.min, yLim.min, width, height );
}
この関数を使って、描画する3次曲線のアクター側に以下のコードを組み込む。
render(target, scroller) {
const context = target.getContext('2d');
context.strokeStyle = this._color;
context.lineWidth = 3;
context.beginPath(); //描画位置の初期化
context.moveTo(this.x + scroller.x, this.y + scroller.y); //曲線のスタート位置を指定
context.bezierCurveTo(this.x1 + scroller.x, this.y1 + scroller.y,
this.x2 + scroller.x, this.y2 + scroller.y,
this.x3 + scroller.x, this.y3 + scroller.y); //制御点1、制御点2、終着点をそれぞれ指定して曲線の軌道を描く
context.stroke(); //軌道に沿って線を引く
context.lineWidth = 1;
context.beginPath(); //ここからaabb矩形も可視化してみる。
const Rect1 = this.hitArea.aabbRect2(0, 1/2), Rect2 = this.hitArea.aabbRect2(1/2, 1);
context.strokeRect(Rect1.left, Rect1.top, Rect1.width, Rect1.height);
context.strokeRect(Rect2.left, Rect2.top, Rect2.width, Rect2.height);
}
まず2分割(' '*)
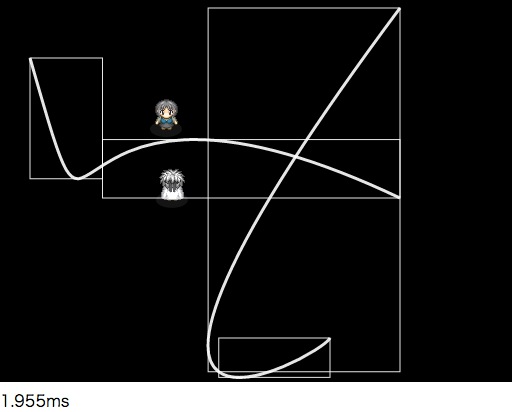
じゃあ次は該当部分を修正しまして(o _ o。)
context.beginPath(); //ここからaabb矩形も可視化してみる。
const Rect1 = this.hitArea.aabbRect2(0, 1/4), Rect2 = this.hitArea.aabbRect2(1/4, 2/4);
const Rect3 = this.hitArea.aabbRect2(2/4, 3/4), Rect4 = this.hitArea.aabbRect2(3/4, 1);
context.strokeRect(Rect1.left, Rect1.top, Rect1.width, Rect1.height);
context.strokeRect(Rect2.left, Rect2.top, Rect2.width, Rect2.height);
context.strokeRect(Rect3.left, Rect3.top, Rect3.width, Rect3.height);
context.strokeRect(Rect4.left, Rect4.top, Rect4.width, Rect4.height);
4分割いきました(。0 _ 0。)ノ
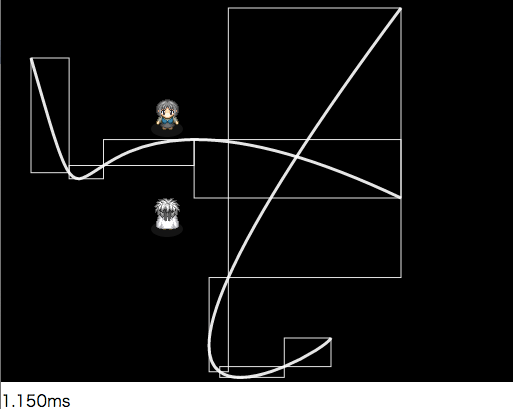
じゃあ今度は8分割で∞
context.beginPath(); //ここからaabb矩形も可視化してみる。
const Rect1 = this.hitArea.aabbRect2(0, 1/8), Rect2 = this.hitArea.aabbRect2(1/8, 2/8);
const Rect3 = this.hitArea.aabbRect2(2/8, 3/8), Rect4 = this.hitArea.aabbRect2(3/8, 4/8);
const Rect5 = this.hitArea.aabbRect2(4/8, 5/8), Rect6 = this.hitArea.aabbRect2(5/8, 6/8);
const Rect7 = this.hitArea.aabbRect2(6/8, 7/8), Rect8 = this.hitArea.aabbRect2(7/8, 1);
context.strokeRect(Rect1.left, Rect1.top, Rect1.width, Rect1.height);
context.strokeRect(Rect2.left, Rect2.top, Rect2.width, Rect2.height);
context.strokeRect(Rect3.left, Rect3.top, Rect3.width, Rect3.height);
context.strokeRect(Rect4.left, Rect4.top, Rect4.width, Rect4.height);
context.strokeRect(Rect5.left, Rect5.top, Rect5.width, Rect5.height);
context.strokeRect(Rect6.left, Rect6.top, Rect6.width, Rect6.height);
context.strokeRect(Rect7.left, Rect7.top, Rect7.width, Rect7.height);
context.strokeRect(Rect8.left, Rect8.top, Rect8.width, Rect8.height);
8分割(。0 _ 0。)ノ ああしまった、矩形の端が被ってて見づらくなってるな。
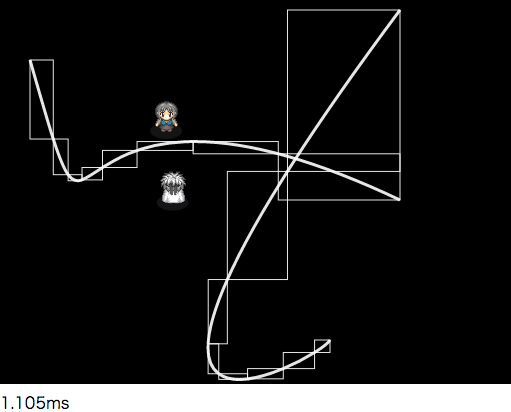
16分割(。0 _ 0。)ノ そろそろ始点と終点を結ぶ対角線が、元の曲線の形に近づいてきたかな?

とまぁ、これが3次曲線と矩形との当たり判定をとるアルゴリズムになります。
大きなaabb矩形とアクターで判定。falseならfalse。trueならさらにaabb矩形を分割。
分割した2つのaabb矩形について同様に判定を行い、両方falseならfalse、片方でもtrueで、さらに始点か終点がアクターと接触してれば当たり。
そうでない場合、trueを返したaabb矩形をさらに分割していずれかの条件と合致するまで繰り返す。。といった感じです。だいたい32分割もすれば、始点と終点を結ぶ直線との最終判定で事足りそうです。
では、そのような当たり判定プログラムを描いてみます。分割数に応じた再帰関数が使われます(' '*)
3次曲線側で分割数の要素を定義して、本番の当たり判定式に行きます。
3次曲線クラス(Collider)に分割数を定義
class BezierCurve extends Collider { //当たり判定を3次曲線で扱うクラス。地形を現す曲線なのでマップに固定。通行判定に使う予定。
constructor(x, y, x1, y1, x2, y2, x3, y3, tag, divNumber=16) {
super('bezierCurve', x, y, tag);
this.x1 = x1; //制御点1のx座標
this.y1 = y1; //制御点1のy座標
this.x2 = x2; //制御点2のx座標
this.y2 = y2; //制御点2のy座標
this.x3 = x3; //終着点のx座標
this.y3 = y3; //終着点のy座標
this.BX3 = this.x3 - this.x + 3*(this.x1 - this.x2); // fx(t) t**3の係数
this.BX2 = this.x2 - 2*this.x1 + this.x; // fx(t) t**2の係数の1/3...使う時は3*BX2として使う。
this.BX1 = this.x1 - this.x; // fx(t) t**1の係数の1/3...使う時は3*BX1として使う。
this.BY3 = this.y3 - this.y + 3*(this.y1 - this.y2); // fy(t) t**3の係数
this.BY2 = this.y2 - 2*this.y1 + this.y; // fy(t) t**2の係数の1/3...使う時は3*BY2として使う。
this.BY1 = this.y1 - this.y; // fy(t) t**1の係数の1/3...使う時は3*BY1として使う。
// X,Yそれぞれが極値となるt値を格納。値は最大2つずつ存在
this.xLimT = [];
this.yLimT = [];
// X,Yの極値となるt値を求める
this.xLimTcheck();
this.yLimTcheck();
// 求めたtの配列から、X,Yの極値の座標を配列に格納する
this.XnoKIWAMI = this.xLimT.map( (t) => this.fx(t) )
this.YnoKIWAMI = this.yLimT.map( (t) => this.fy(t) )
this.divNumber = divNumber; //曲線の当たり判定の分割数。多いほど精度が向上するが、処理が遅くなる。2の累乗係数◎。だいたい32が適正か?
再帰関数を使った3次曲線との当たり判定
deRectBezierCurve(Rect, bezierCurve) { //矩形と3次ベジェ曲線の当たり判定導入部
if( !this.deRectRect(Rect, bezierCurve.aabbRect) ) {return false;}
const timeCurve = [];
if( this.deRectPoint(Rect, bezierCurve.x, bezierCurve.y) ) {return [0];} //始点判定、trueならt=0で当たり。
if( this.deRectPoint(Rect, bezierCurve.x3, bezierCurve.y3) ) {return [1];} //終点判定、trueならt=1で当たり。
return this.deRectBezierCurve1_2(Rect, bezierCurve, 0, 1); //それ以外なら始点t=0から終点t=1までの曲線を2分割してそれぞれのaabb判定から繰り返し
}
deRectBezierCurve1_2(Rect, bezierCurve, t0, t1) { //矩形と、t0〜t1までを2分割した3次曲線との当たり判定、再帰関数
const t0_5 = t0 + (t1 - t0) *0.5; // t範囲の半分の位置を定義
if( t1 - t0 >= 2/bezierCurve.divNumber ) { // 分割数が余裕あるなら、tの範囲を2分割してaabb判定を繰り返す
const bezierRect1 = bezierCurve.aabbRect2(t0, t0_5);
const bezierRect2 = bezierCurve.aabbRect2(t0_5, t1);
if( this.deRectPoint(Rect, bezierCurve.fx(t0_5), bezierCurve.fy(t0_5)) ) { return [t0_5];} //中間地点の座標点と接触するなら当たり!
if( !this.deRectRect(Rect, bezierRect1) && !this.deRectRect(Rect, bezierRect2) ) {return false;} //両方のaabb矩形がfalseならfalse判定
else if( this.deRectRect(Rect, bezierRect1) && !this.deRectRect(Rect, bezierRect2) ) { //片方のaabbでtrueなら、さらに2分割して調査
return this.deRectBezierCurve1_2(Rect, bezierCurve, t0, t0_5);
}
else if( !this.deRectRect(Rect, bezierRect1) && this.deRectRect(Rect, bezierRect2) ) { //片方のaabbでtrueなら、さらに2分割して調査
return this.deRectBezierCurve1_2(Rect, bezierCurve, t0_5, t1);
}
else { //両方のaabbでtrueなら、それぞれをさらに2分割して調査
return (this.deRectBezierCurve1_2(Rect, bezierCurve, t0, t0_5) || this.deRectBezierCurve1_2(Rect, bezierCurve, t0_5, t1));
}
}
else { // 分割数の限界まで達したら、最後は直線で判定
const bezierLine = new Line(bezierCurve.fx(t0), bezierCurve.fy(t0), bezierCurve.fx(t1), bezierCurve.fy(t1));
if(this.deRectLine(Rect, bezierLine)) {return [t0_5];}
return false; // 最後の直線でfalseか、分割した2つのaabb矩形ともfalse判定なら、falseで終了
}
}
とりあえずこんなもんでしょ(。0 _ 0。)ノ 当たったらその場でt値を返して終了。
という感じで描いてみた。動く、動きますよ〜。当たる、判定有りですよ〜〜〜!!
3次曲線とのバウンド処理(反動ベクトルをActorに適用)
if( other.type=='bezierCurve') { //3次曲線とのバウンス判定
const t = e.info; // 交点となるtの解を得る、このtから法線ベクトルを求める
//const otherCx = other.fx(t), otherCy = other.fy(t); 曲線上のバウンドの起点となるXとYの座標を求める
const delta = new Vector2D (this.hitArea.cx - other.fx(t), this.hitArea.cy - other.fy(t)); //曲線上のバウンドの起点から自分の中心点までのベクトルで、お互いの位置関係を取得
const bounceVect = other.bounceVect(t).normalVect; // 法線の単位ベクトルを取得する(バウンド方向)
if(bounceVect.innerP(delta) < 0) {bounceVect.dx*=-1; bounceVect.dy*=-1;} // もし法線が逆さ(内積が負)なら、ベクトルを逆向きにする。
if ( this.speed*this.speed < this.vector.length2 ) { speed = this.vector.length; } //もし自分の移動ベクトルが(押し戻しなどの影響で)自分の速度より大きくなってるなら、移動ベクトルの大きさを反動の大きさとする。
this._velocityX += speed * bounceVect.dx; //X軸の反動の大きさを反映
this._velocityY += speed * bounceVect.dy; //Y軸の反動の大きさを反映
return;
}
2次曲線と同じように、3次曲線とのバウンド処理もSpriteActorに仕込んどいて、デモを見てみます。
どうでしょう。いい感じですね。
しかし、一番凹んでる部分に抜け穴が...これじゃ通行判定の壁に使えんくなる。。厳密な衝突地点じゃないから法線がズレるんだよね。
なので、当たり判定のコードを見直し。当たったら即returnではなく、衝突地点のtを継続して記録してみよう(。0 _ 0。)ノ
ということで、こんなふうに姉妹sた・・・
最後まで判定して、当たってる曲線のt地点を複数取得します。
3次ベジェ曲線との当たり判定改定後
deRectBezierCurve(Rect, bezierCurve) { //矩形と3次ベジェ曲線の当たり判定導入部
if( !this.deRectRect(Rect, bezierCurve.aabbRect) ) {return false;}
const timeCurve = []; // 交点となるtの値をリストに格納する
if( this.deRectPoint(Rect, bezierCurve.x, bezierCurve.y) ) {timeCurve.push(0); return timeCurve;} //始点判定、trueならt=0で当たり。
if( this.deRectPoint(Rect, bezierCurve.x3, bezierCurve.y3) ) {timeCurve.push(1); return timeCurve;} //終点判定、trueならt=1で当たり。
this.deRectBezierCurve1_2(Rect, bezierCurve, 0, 1, timeCurve); //それ以外なら始点t=0から終点t=1までの曲線を2分割してそれぞれのaabb判定から繰り返し
if( timeCurve.length > 0 ) { console.log(timeCurve); return timeCurve;} // 交点となるtが存在するなら、そのリストを返す(true判定)
return false;
}
deRectBezierCurve1_2(Rect, bezierCurve, t0, t1, timeCurve) { //矩形と、t0〜t1までを2分割した3次曲線との当たり判定、再帰関数
const t0_5 = t0 + (t1 - t0) *0.5; // t範囲の半分の位置を定義
if( (t1 - t0) *bezierCurve.divNumber >= 2 ) { // 分割数が余裕あるなら、tの範囲を2分割してaabb判定を繰り返す
const bezierRect1 = bezierCurve.aabbRect2(t0, t0_5);
const bezierRect2 = bezierCurve.aabbRect2(t0_5, t1);
const i = t0_5 *bezierCurve.divNumber;
if( this.deRectPoint(Rect, bezierCurve.tArray[i].x, bezierCurve.tArray[i].y) ) { timeCurve.push(t0_5); } //中間地点の座標点と接触するなら当たり!
if( this.deRectRect(Rect, bezierRect1) ) { this.deRectBezierCurve1_2(Rect, bezierCurve, t0, t0_5, timeCurve); } //分割した矩形と接触するならさらにそれを2分割
if( this.deRectRect(Rect, bezierRect2) ) { this.deRectBezierCurve1_2(Rect, bezierCurve, t0_5, t1, timeCurve); } //同上
}
else { // 分割数の限界まで達したら、最後は直線で判定
const i0 = t0*bezierCurve.divNumber, i1 = t1*bezierCurve.divNumber;
const bezierLine = new Line(bezierCurve.tArray[i0].x, bezierCurve.tArray[i0].y, bezierCurve.tArray[i1].x, bezierCurve.tArray[i1].y);
if(this.deRectLine(Rect, bezierLine)) {timeCurve.push(t0_5);}
}
}
衝突地点tを格納する配列を定義した'timeCurve'を、各関数に渡して引き継がせてるのがポイントでしょうか。 それと、t地点の座標を格納(計算結果を保存しておく、後の章で解説予定)を改良して、少々計算スピードを早めてみました。
あとは、バウンス処理の方で各t地点から平均を取り、法線ベクトルを求めてバウンスさせます。
3次曲線とのバウンド処理 改良後
if( other.type=='bezierCurve') { //3次曲線とのバウンス判定
const tSum = e.info.reduce((a, c) => a + c); // 交点となるtの解の和(複数の場合)
const t = tSum / e.info.length; // tの解の平均値を得る、このtから法線ベクトルを求める
//const otherCx = other.fx(t), otherCy = other.fy(t); 曲線上のバウンドの起点となるXとYの座標を求める
const delta = new Vector2D (this.hitArea.cx - other.fx(t), this.hitArea.cy - other.fy(t)); //曲線上のバウンドの起点から自分の中心点までのベクトルで、お互いの位置関係を取得
const bounceVect = other.bounceVect(t).normalVect; // 法線の単位ベクトルを取得する(バウンド方向)
if(bounceVect.innerP(delta) < 0 && !e.target.isFall) {bounceVect.dx*=-1; bounceVect.dy*=-1;} // もし法線が逆さ(内積が負)なら、ベクトルを逆向きにする。
if ( this.speed*this.speed < this.vector.length2 ) { speed = this.vector.length; } //もし自分の移動ベクトルが(押し戻しなどの影響で)自分の速度より大きくなってるなら、移動ベクトルの大きさを反動の大きさとする。*/
this._velocityX += speed * bounceVect.dx *1.0625; //X軸の反動の大きさを反映 乗り越えを防ぐのに、反動の大きさ一割増し。
this._velocityY += speed * bounceVect.dy *1.0625; //Y軸の反動の大きさを反映
}
抜け穴対策その2として、法線ベクトルの大きさを単位ベクトルから1/16分増しにしました。
これで安定した感じです(' '*)
抜け穴がなくなりました(。◕ ∀ ◕。)ノ
ここまでで3次ベジェ曲線まで、無事クリア。
2次関数の解の公式、微分、ベクトル、キャッシュの扱い方、再帰関数、目的にかなったアルゴリズムのコードを選択する。など、かなり高難度なチャレンジになってしまいましt。
曲線をマップで使いたいがために粘りましたが、これだけで1ヶ月以上も費やす有様。学習コストが高いですね。
でもまぁ、色々学べたのでよしとします。特に直線から曲線に至る数式の配列とか、キャッシュとか、芸術めいた部分を感じておりました。この辺は曲線使わないにしろ知ってると色々お得です。
なので次項、直線の式の補足と、キャッシュの扱いについて少し触れてみたいと思います。
サポートくださった古都先生、ありがとうございます><
次回は休憩がてら、曲線当たり判定の整理と気付きについてメモします。
⇒ JavaScriptでゲーム作り「10EX:線分とベジェ曲線の数式を最適化する」
すぺしゃるさんくす
古都さんのフレームワークを元にほぼ最初から作ってます。
たぶん順番に見ないとちんぷんかんぷん(' '*)...
https://sbfl.net/
古都さん
JavaScriptで作る弾幕STGの基礎(フレームワーク)を使わせていただいてます。感謝!

ぴぽやさんもありがとう、キャラチップをお借りしています。