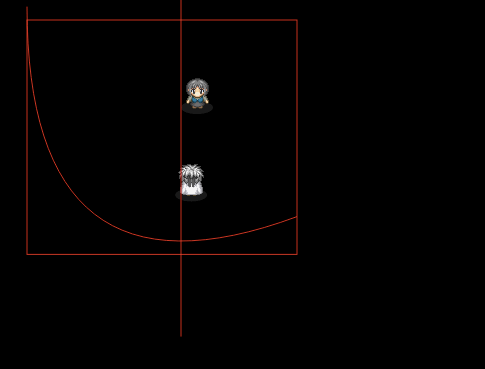
10:法線ベクトルとバウンス処理
矩形と円、線分との当たり判定後のバウンス処理に関して、完成デモはこんな感じです。
⇒ 移動する壁のデモを見る
Hit判定時のバウンス処理を実装する
(2019.4.07執筆)
これまでのバウンス処理は、単に操作キャラの移動スピード分だけ、ぶつかった方向の反対側に押し戻すだけでした。また、形状による分岐も深く考えず、とりあえず実装した形でした。
もし動いてるのが操作キャラのみであれば良いのですが、ぶつかった相手が動いてる場合に、その移動ベクトルをどのように反映させれば良いのか?ということもきちんと考えておきたい。
ここで、アクター同士がぶつかった時のバウンス処理の関数を、丁寧に見直していきます。
(比重とか反発係数とかオブジェクトの回転など、余計な要素は未だ考えないことにします。基本ができてないので)
バウンス処理を考える手順
- ステップ0(ベクトル要素を定義して、各アクターに持たせる)
- ステップ1(Hit判定時のバウンス方向(法線ベクトル)を求める式)
- 矩形との衝突の場合
- 円形との衝突の場合
- 線分との衝突の場合
- ステップ2(衝突相手にも移動ベクトルが存在するとき、どう反映させるか)
- 矩形相手の移動ベクトル
- 円形相手の移動ベクトル
- 線分相手の移動ベクトル
順に考えていきます。まずベクトルの定義から。
Vector2Dクラスを新しく定義する
class Vector2D { // ベクトル計算に使うクラス。Lineクラスの縮小版。衝突時のバウンス判定に用いる。
constructor(dx, dy) {
this.dx = dx;
this.dy = dy;
}
get length() { return Math.sqrt( this.dx * this.dx + this.dy * this.dy ); } // ベクトルの大きさを求める(三平方の定理より)
get length2() { return this.dx * this.dx + this.dy * this.dy; } // ベクトルの大きさの2乗を求める(大きさを比較するときに使う...平方計算を省略して高速化)
get normalVect() { const length = this.length; return new Vector2D( this.dx / length, this.dy / length ); } //単位ベクトルを返す
innerP(other) { return this.dx * other.dx + this.dy * other.dy; } //他のベクトルとの内積
crossP(other) { return this.dx * other.dy - other.dx * this.dy; } //他のベクトルとの外積
crossAB(x, y) { return this.dx * (this.y - y) - this.dy * (this.x - x); } //他の点との位置関係...0ならベクトルの延長上に点が重なる
}
ベクトル要素は前回までLine(Collider)クラスに組み込んでいましたが、ベクトル単体で使えた方が良いかな?と思い、Lineクラスのベクトル用メソッドを引き継いだ状態で、新しく追加してます。
(dx = X軸の移動量, dy = Y軸の移動量)という二つの値で成り立つ。dxが正のときは右に、負のときは左に向かっており、dyが正のときは下に、負のときは上に向かってます。
なおnew Vector2D(0,0)のときは、止まったまま動いてません...
Line(Collider)クラスのbounceVect()関数を修正
get bounceVect() { const length = this.length; return new Vector2D( this.dy / length, - this.dx / length ); } //法線ベクトルを正でとる
get bounceVect_() { const length = this.length; return new Vector2D( - this.dy / length, this.dx / length ); } //法線ベクトルを負でとる
Vector2Dクラスを作ったので、ついでに、Line(Collider)クラスの法線ベクトルを求める関数を、単に{dx,dy}の値を返すのではなく、このVector2Dクラスをreturnできるようにすると、ベクトルの内積や外積の計算にも活用できていい感じです。
あと、2点間を結んだ線分を単位ベクトルに変換する関数も用意しておきます。円とのバウンス処理のとき、円の中心から自分の中心点までのバウンス方向を求めるときに使います。
get normalVect() { const length = this.length; return new Vector2D( this.dx / length, this.dy / length ); } //この線分の単位ベクトルを返す
Actorクラスにベクトル要素を追加
class Actor extends EventDispatcher {//EventDispatcherイベント発生関数を持つActorクラスの定義
constructor(x, y, hitArea, tags = []) {
super();
this.hitArea = hitArea;
this._hitAreaOffsetX = hitArea.x;
this._hitAreaOffsetY = hitArea.y;
this.tags = tags;
this.x = x;
this.y = y;
this.vector = new Vector2D( 0, 0 ); //現在フレームの移動ベクトルを格納、初期値(0, 0)
}
次にActorクラスに対して、このアクターの移動ベクトルを格納するthis.vectorを追加します。
this.vector = new Vector2D( 0, 0 ); // フレーム毎の移動ベクトルを格納するための要素。初期値は(0, 0)です。
hit判定時にはアクターの総当りになるので、相手のベクトルに応じた衝突時の反動を求めるとき参照できたら良いなと思って。基本0で記述を加えてます。
PlayerクラスやSpriteActorなどの、各アクターのupdate()内に追記
update(gameInfo, input, touch) {
// update内で色々やった後の最後に
this.vector = new Vector2D( this._velocityX, this._velocityY ); //現在フレームの移動ベクトルを格納。
this._velocityX = 0;//アップデートの最後にx軸の移動距離をリセット
this._velocityY = 0;//アップデートの最後にy軸の移動距離をリセット
}
this.vectorは各アクターの毎フレームアップデート時に、new Vector2D( this._velocityX, this._velocityY );として、現フレームの移動ベクトルを格納する役目を果たします。(フレーム更新した後、各移動値が0にリセットするが、this.vectorに格納すると次のフレーム更新まで値を保存できる。)
これは衝突相手の移動ベクトルまで反映させるとき必要になってくるので、動くActorクラスには忘れず追記しておきます。
さて、衝突判定のときにベクトルを参照する準備が整いました。本番のバウンス判定に移ります。
Hit判定時のバウンス(反動ベクトル)を求める式について
this.addEventListener('hit', (e) => { //当たり判定発生時のバウンス判定
if(!e.target.hasTag('playerAction') && !e.target.hasTag('event') && !e.target.hasTag('spirit') && !e.target.hasTag('element')) { //これらのタグ相手とはバウンス判定しない。
const other = e.target.hitArea;
let speed = this.speed; //反動ベクトルの大きさを定義する。基本はこのアクターの速さ。
if( this.isHit < 12 ) { this.isHit = 12; }
if( other.type == 'rectangle') { //矩形とのバウンス判定
const dx = this.hitArea.cx - other.cx; //お互いの中心座標(x軸)で位置関係を把握。正の値ならこのアクターが右側
const dy = this.hitArea.cy - other.cy; //お互いの中心座標(y軸)で位置関係を把握。正の値ならこのアクターが下側
let boundWidth = 0, boundHeight = 0; //重なってる部分の幅と高さを定義
if (dx < 0) { boundWidth = this.hitArea.right - other.left; } //dx = 負の値ならこのアクターが左側。自分の右端から、相手の左端を引いた値が重なりの幅。
else if (dx > 0) { boundWidth = other.right - this.hitArea.left; } //dx = 正の値ならこのアクターが右側。相手の右端から、自分の左端を引いた値が重なりの幅。
if (dy < 0) { boundHeight = this.hitArea.bottom - other.top; } //dy = 負の値ならこのアクターが上側。自分の下端から、相手の上端を引いた値が重なりの高さ。
else if (dy > 0) { boundHeight = other.bottom - this.hitArea.top; } //dy = 正の値ならこのアクターが下側。相手の下端から、自分の上端を引いた値が重なりの高さ。
if (boundWidth <= boundHeight + 3) { // 横の重なりより縦の重なりが大きいなら、横の衝突。誤差3ピクセルまで許容
if (dx < 0) { this._velocityX += -speed; } // dx = 負の値ならこのアクターが左側。左にバウンス
else if (dx > 0) { this._velocityX += speed; } // dx = 正の値ならこのアクターが右側。右にバウンス。
}
if (boundHeight <= boundWidth + 3) { // 縦の重なりより横の重なりが大きいなら、縦の衝突。誤差3ピクセルまで許容
if (dy < 0) { this._velocityY += -speed; } // dy = 負の値ならこのアクターが上側、上にバウンス
else if (dy > 0) { this._velocityY += speed; } // dy = 正の値ならこのアクターが下側、下にバウンス
}
return;
}
if( other.type == 'circle') { //円形とのバウンス判定。
const bounceVect = new Vector2D(this.hitArea.cx - other.cx, this.hitArea.cy - other.cy).normalVect; //相手の中心座標から自分の中心座標に向かうバウンス方向を単位ベクトルで求める
this._velocityX += speed * bounceVect.dx; //このアクターの速さに法線の単位ベクトルX軸をかけて反映
this._velocityY += speed * bounceVect.dy; //このアクターの速さに法線の単位ベクトルY軸をかけて反映
return;
}
if( other.type=='line') { //壁、線分とのバウンス判定
const lineAB = e.target.hitArea; //ライン壁を定義
const delta = lineAB.crossAB(this.hitArea.cx, this.hitArea.cy); // このアクターは、ラインのどちら側に居るか?
let bounceVect; //法線ベクトル(衝突時の反動の方向)を定義する文字列。
if(e.target.isFall === true || delta > 0) { bounceVect = lineAB.bounceVect; } //deltaが正のとき、あるいは一方通行のとき、ラインの法線ベクトルを正でとる。
else { bounceVect = lineAB.bounceVect_; } //deltaが負のとき、ラインの法線ベクトルを負でとる。
this._velocityX += speed * bounceVect.dx; //X軸の反動の大きさを反映
this._velocityY += speed * bounceVect.dy; //Y軸の反動の大きさを反映
return;
}
}
});
ベースとなるHit時のバウンス判定式(どちら側にどれだけ移動させるか)を、大元のSpriteActorに割り当てました。
ぶつかった時の反動ベクトルを計算するだけなのですが。。。相手アクターの形状とか条件で振り分ける必要があるので、ちょと長くなりました。形状ごとに分けてみていきましょう。
- すり抜けていいアクターのタグを確認して、当てはまったら何もしない(ただのイベント判定とか)
- 自分の移動スピードを取得する
- ぶつかる判定をisHitに加算(ダッシュ移動を普通の歩行スピードに減速させる目的)
- 各形状に振り分け。反動ベクトルの式をそれぞれ記し、バウンス。
- 相手が矩形の場合
- 相手が円形の場合
- 相手が線分(壁)の場合
この手順、とりあえず相手が動いてない前提で考えます(分かりやすいので)
では、形状の式を1つずつ確認していきたいと思います。ちなみにSpriteActor(自分の形状)は矩形を基本としています。
現在の自分の移動スピードを取得
let speed = this.speed; //反動ベクトルの大きさを定義する文字列
この値が、反動ベクトルの大きさとなります。
※このアクターの速さを習得する式
get speed() {
if(this.isStand) {return 0;} //立ち止まってる時の移動スピードは0
if(this.isHit === 0) { return (this.walkSpeed + this.isDash * 4); } //移動スピードを取得。ダッシュ中はベース値に+4、
else {return this.walkSpeed;} //Hit判定時は歩行スピード
}
速さを求める関数は、同クラス内に記載しています。
Hit判定時に、isHitに加算
if( this.isHit < 12 ) { this.isHit = 12; }
これは、現在Hit中かどうかを参照するための値です。
この値が存在する限り、Hit判定中として条件分岐ができるようになります。
例えばダッシュ中であるかどうかに関わらず、Hit中は速度が歩行スピードになります。
true、falseでなくカウント式になってるのは、硬直時間?みたいなのを設けるためです。
各フレーム毎に1ずつ減少し、0でHit判定が解除されます。
※このアクターについて、フレーム毎のupdate()後にisHit値の減少
if(this.isHit !== 0) {this.isHit -= 1;} // ここでHit判定値を1減少
とまぁ、衝突判定に必要な値(このアクターの速さ)が得られたので、各形状の分岐に移ります。
相手が矩形の場合のバウンス判定
if( other.type == 'rectangle') { //矩形とのバウンス判定
const dx = this.hitArea.cx - other.cx; //お互いの中心座標(x軸)で位置関係を把握。正の値ならこのアクターが右側
const dy = this.hitArea.cy - other.cy; //お互いの中心座標(y軸)で位置関係を把握。正の値ならこのアクターが下側
let boundWidth = 0, boundHeight = 0; //重なってる部分の幅と高さを定義
if (dx < 0) { boundWidth = this.hitArea.right - other.left; } //dx = 負の値ならこのアクターが左側。自分の右端から、相手の左端を引いた値が重なりの幅。
else if (dx > 0) { boundWidth = other.right - this.hitArea.left; } //dx = 正の値ならこのアクターが右側。相手の右端から、自分の左端を引いた値が重なりの幅。
if (dy < 0) { boundHeight = this.hitArea.bottom - other.top; } //dy = 負の値ならこのアクターが上側。自分の下端から、相手の上端を引いた値が重なりの高さ。
else if (dy > 0) { boundHeight = other.bottom - this.hitArea.top; } //dy = 正の値ならこのアクターが下側。相手の下端から、自分の上端を引いた値が重なりの高さ。
if (boundWidth <= boundHeight + 3) { // 横の重なりより縦の重なりが大きいなら、横の衝突。誤差3ピクセルまで許容
if (dx < 0) { this._velocityX += -speed; } // dx = 負の値ならこのアクターが左側。左にバウンス
else if (dx > 0) { this._velocityX += speed; } // dx = 正の値ならこのアクターが右側。右にバウンス。
}
if (boundHeight <= boundWidth + 3) { // 縦の重なりより横の重なりが大きいなら、縦の衝突。誤差3ピクセルまで許容
if (dy < 0) { this._velocityY += -speed; } // dy = 負の値ならこのアクターが上側、上にバウンス
else if (dy > 0) { this._velocityY += speed; } // dy = 正の値ならこのアクターが下側、下にバウンス
}
return;
}
相手が矩形の場合、最初にお互いの中心座標を比較して、位置関係を確認できるようにします。
const dx = this.hitArea.cx - other.cx; //お互いの中心座標(x軸)で位置関係を把握。正の値ならこのアクターが右側
const dy = this.hitArea.cy - other.cy; //お互いの中心座標(y軸)で位置関係を把握。正の値ならこのアクターが下側
dx > 0 なら、このアクターが右。相手が左。
dx < 0 なら、このアクターが左。相手が右。
dyの方も同じ感覚で、上下左右の位置関係が何となく分かります。
んで、もうhit判定はtrueで帰ってきてる。どれかの辺が接してるのは確実。
よって、矩形同士の重なり合う部分が間違いなく存在するので、その重なってる部分の幅と高さを求めてしまいます。
let boundWidth = 0; //重なってる部分の幅を定義
if (dx < 0) { boundWidth = this.hitArea.right - other.left; } //dx = 負の値ならこのアクターが左側。自分の右端から、相手の左端を引いた値が重なりの幅。
else if (dx > 0) { boundWidth = other.right - this.hitArea.left; } //dx = 正の値ならこのアクターが右側。相手の右端から、自分の左端を引いた値が重なりの幅。
let boundHeight = 0; //重なってる部分の高さを定義
if (dy < 0) { boundHeight = this.hitArea.bottom - other.top; } //dy = 負の値ならこのアクターが上側。自分の下端から、相手の上端を引いた値が重なりの高さ。
else if (dy > 0) { boundHeight = other.bottom - this.hitArea.top; } //dy = 正の値ならこのアクターが下側。相手の下端から、自分の上端を引いた値が重なりの高さ。
まずX軸の判定ですが、(dx < 0?)お互いの位置関係によって式が変わっている感じです。図にすると分かりやすいけど。イメージで。
もし自分が左側にいるなら(dx < 0)、自分の右端から相手の左端までが重なってます。よって、重なりの幅は{boundWidth = this.hitArea.right - other.left;}で求められる。
もし相手が左側にいるなら(dx > 0)、相手の右端から自分の左端までの距離を求めれば、重なりの幅が求まります。 { boundWidth = other.right - this.hitArea.left; }
高さの方も同様に、y軸の判定で求めることができます。
- 重なりの部分が縦に長ければ、左右のぶつかり合い。
- 重なりの部分が横に長ければ、上下のぶつかり合い。
重なる部分が正方形に近づくほど、斜め方向にぶつかってる感覚がイメージされそうです。
あとは、左右と上下のどちらに反動が働くかを条件分けして、自分の移動スピード分だけバウンスさせればOKです。
if (boundWidth <= boundHeight + 3) { // 横の重なりより縦の重なりが大きいなら、横の衝突。誤差3ピクセルまで許容
if (dx < 0) { this._velocityX += -speed; } // dx = 負の値ならこのアクターが左側。左にバウンス
else if (dx > 0) { this._velocityX += speed; } // dx = 正の値ならこのアクターが右側。右にバウンス。
}
if (boundHeight <= boundWidth + 3) { // 縦の重なりより横の重なりが大きいなら、縦の衝突。誤差3ピクセルまで許容
if (dy < 0) { this._velocityY += -speed; } // dy = 負の値ならこのアクターが上側、上にバウンス
else if (dy > 0) { this._velocityY += speed; } // dy = 正の値ならこのアクターが下側、下にバウンス
}
相手が円形の場合のバウンス判定
if( other.type == 'circle') { //円形とのバウンス判定。
const bounceVect = new Vector2D(this.hitArea.cx - other.cx, this.hitArea.cy - other.cy).normalVect; //相手の中心座標から自分の中心座標に向かうバウンス方向を単位ベクトルで求める
this._velocityX += speed * bounceVect.dx; //このアクターの速さに法線の単位ベクトルX軸をかけて反映
this._velocityY += speed * bounceVect.dy; //このアクターの速さに法線の単位ベクトルY軸をかけて反映
return;
}
相手が円の場合は簡単です。相手の中心点と、自分の中心点との位置関係から、どの方向にバウンスさせるか?のベクトルが分かります。
あとは、単位ベクトル(求めたベクトルをその距離で割る)に自分の移動スピードを掛けた分だけx軸の移動とy軸の移動をさせればいいです。
相手が線分(壁)の場合のバウンス判定
if( other.type=='line') { //壁、線分とのバウンス判定
const lineAB = e.target.hitArea; //ライン壁を定義
const delta = lineAB.crossAB(this.hitArea.cx, this.hitArea.cy); // このアクターは、ラインのどちら側に居るか?
let bounceVect; //法線ベクトル(衝突時の反動の方向)を定義する文字列。
if(e.target.isFall === true || delta > 0) { bounceVect = lineAB.bounceVect; } //deltaが正のとき、あるいは一方通行のとき、ラインの法線ベクトルを正でとる。
else { bounceVect = lineAB.bounceVect_; } //deltaが負のとき、ラインの法線ベクトルを負でとる。
this._velocityX += speed * bounceVect.dx; //X軸の反動の大きさを反映
this._velocityY += speed * bounceVect.dy; //Y軸の反動の大きさを反映
return;
}
ラインとのバウンス判定式の解説は、線分の衝突判定のページに載せてます。
ラインと衝突した時にどちら向きにバウンスさせるか?の判定が肝です。
詳しく ⇒ JavaScriptでゲーム作り「6:線分の当たり判定を実装する」
ここまでで基本となるバウンス判定が書けました。
相手が動いてない前提 + バウンスベクトルの大きさを自分のspeedで固定。
ひとまず、前項のChapter9までの判定式は、このような感じで描けております。
相手の移動ベクトルを衝突判定に反映させる式
次に、衝突相手の移動ベクトルの反映です。
このアクターの速さとは別に判定します。
というのも衝突が起こった場合の、実際の速さと移動ベクトルの大きさは必ずしも等しいわけではないから。自分と相手のベクトル同士を合わせると計算できなくなってしまいます。
しかし、自分からぶつかった時の反動ベクトルは綺麗に反映出来たので、ここに相手の移動ベクトルの方向を調べ、条件が合えば加算する形でOKな感じになりました。
相手の移動ベクトルの反映についての手順
- 法線ベクトル(バウンスの方向)と、相手の移動ベクトルの方向とを比べる(ベクトルの内積で計算)
- もし内積が正の値なら、相手の移動ベクトルそのままthis._Vellocityに加算する
- もし内積が負の値なら何もしない(バウンスの方向と相手の移動ベクトルは反対方向にむいてるので)
各形状とも、だいたいこんな感じです。
SpriteActorに記述する衝突バウンス判定式の完成形
this.addEventListener('hit', (e) => { //当たり判定発生時のバウンス判定
if(!e.target.hasTag('playerAction') && !e.target.hasTag('event') && !e.target.hasTag('floar') && !e.target.hasTag('element')) { //これらのタグ相手とはバウンス判定しない。
const other = e.target.hitArea;
let speed = this.speed; //反動ベクトルの大きさを定義する。基本はこのアクターの速さ。
if( this.isHit < 12 ) { this.isHit = 12; }
if( other.type == 'rectangle') { //矩形とのバウンス判定
const dx = this.hitArea.cx - other.cx; //お互いの中心座標(x軸)で位置関係を把握。正の値ならこのアクターが右側
const dy = this.hitArea.cy - other.cy; //お互いの中心座標(y軸)で位置関係を把握。正の値ならこのアクターが下側
let boundWidth = 0, boundHeight = 0; //重なってる部分の幅と高さを定義
if (dx < 0) { boundWidth = this.hitArea.right - other.left; } //dx = 負の値ならこのアクターが左側。自分の右端から、相手の左端を引いた値が重なりの幅。
else if (dx > 0) { boundWidth = other.right - this.hitArea.left; } //dx = 正の値ならこのアクターが右側。相手の右端から、自分の左端を引いた値が重なりの幅。
if (dy < 0) { boundHeight = this.hitArea.bottom - other.top; } //dy = 負の値ならこのアクターが上側。自分の下端から、相手の上端を引いた値が重なりの高さ。
else if (dy > 0) { boundHeight = other.bottom - this.hitArea.top; } //dy = 正の値ならこのアクターが下側。相手の下端から、自分の上端を引いた値が重なりの高さ。
if (boundWidth <= boundHeight + 3) { // 横の重なりより縦の重なりが大きいなら、横の衝突。誤差3ピクセルまで許容
if (dx < 0) { this._velocityX += -speed; // dx = 負の値ならこのアクターが左側。左にバウンス
if ( e.target.vector.dx < 0 ) { this._velocityX += e.target.vector.dx; } //相手が左側に移動してる時、その分を自分も移動する。
}
else if (dx > 0) { this._velocityX += speed; // dx = 正の値ならこのアクターが右側。右にバウンス。
if ( e.target.vector.dx > 0 ) { this._velocityX += e.target.vector.dx; } //相手が右側に移動してる時、その分を自分も移動する。
}
}
if (boundHeight <= boundWidth + 3) { // 縦の重なりより横の重なりが大きいなら、縦の衝突。誤差3ピクセルまで許容
if (dy < 0) { this._velocityY += -speed; // dy = 負の値ならこのアクターが上側、上にバウンス
if ( e.target.vector.dy < 0 ) { this._velocityY += e.target.vector.dy; } //相手が上側に移動してる時、その分を自分も移動する。
}
else if (dy > 0) { this._velocityY += speed; // dy = 正の値ならこのアクターが下側、下にバウンス
if ( e.target.vector.dy > 0 ) { this._velocityY += e.target.vector.dy; } //相手が下側に移動してる時、その分を自分も移動する。
}
}
return;
}
if( other.type == 'circle') { //円形とのバウンス判定
const bounceVect = new Vector2D(this.hitArea.cx - other.cx, this.hitArea.cy - other.cy).normalVect; //相手の中心座標から自分の中心座標に向かうバウンス方向を単位ベクトルで求める
this._velocityX += speed * bounceVect.dx; //このアクターの速さに法線の単位ベクトルX軸をかけて反映
this._velocityY += speed * bounceVect.dy; //このアクターの速さに法線の単位ベクトルY軸をかけて反映
if ( e.target.vector.innerP(bounceVect) > 0 ) { //法線ベクトルと、相手の移動ベクトルの内積が正の値なら、相手の移動ベクトルも反映。
this._velocityX += e.target.vector.dx;
this._velocityY += e.target.vector.dy;
}
return;
}
if( other.type=='line') { //壁、線分とのバウンス判定
const lineAB = e.target.hitArea; //ライン壁を定義
const delta = lineAB.crossAB(this.hitArea.cx, this.hitArea.cy); // このアクターは、ラインのどちら側に居るか?
let bounceVect; //法線ベクトル(衝突時の反動の方向)を定義する文字列。
if(e.target.isFall === true || delta > 0) { bounceVect = lineAB.bounceVect; } //deltaが正のとき、あるいは一方通行のとき、ラインの法線ベクトルを正でとる。
else { bounceVect = lineAB.bounceVect_; } //deltaが負のとき、ラインの法線ベクトルを負でとる。
if ( this.speed*this.speed < this.vector.length2 ) { speed = this.vector.length; } //もし自分の移動ベクトルが(押し戻しなどの影響で)自分の速度より大きくなってるなら、移動ベクトルの大きさを反動の大きさとする。
this._velocityX += speed * bounceVect.dx; //X軸の反動の大きさを反映
this._velocityY += speed * bounceVect.dy; //Y軸の反動の大きさを反映
//ここから衝突したライン側の移動ベクトルを反映させるかテスト
if ( e.target.vector.dx !== 0 || e.target.vector.dy !== 0 ) {//ラインの移動ベクトルが0ではないとき
const lineAP = new Line(e.target.hitArea.x, e.target.hitArea.y, this.hitArea.cx, this.hitArea.cy); //ラインの始点から自分の中心点に線を引く
const innerAX = lineAB.innerP(lineAP); //ラインの法線上に自分の中心点があるかどうか?に使う内積の値
if(0 <= innerAX && innerAX <= lineAB.length2) { // ラインの始点から終点までの法線上に、自分の中心点がある! 次の判定式へ
if ( e.target.vector.innerP(bounceVect) > 0 ) { // さらにラインの法線ベクトルと、ラインの移動ベクトルの内積が正の値なら、ラインの移動ベクトルも反映。
this._velocityX += e.target.vector.dx;
this._velocityY += e.target.vector.dy;
}
}
}
return;
}
}
});
では、もう一度矩形の場合から見ていきたいと思います。
相手が矩形の場合の衝突判定式(相手の移動ベクトル含む)
if( other.type == 'rectangle') { //矩形とのバウンス判定
const dx = this.hitArea.cx - other.cx; //お互いの中心座標(x軸)で位置関係を把握。正の値ならこのアクターが右側
const dy = this.hitArea.cy - other.cy; //お互いの中心座標(y軸)で位置関係を把握。正の値ならこのアクターが下側
let boundWidth = 0, boundHeight = 0; //重なってる部分の幅と高さを定義
if (dx < 0) { boundWidth = this.hitArea.right - other.left; } //dx = 負の値ならこのアクターが左側。自分の右端から、相手の左端を引いた値が重なりの幅。
else if (dx > 0) { boundWidth = other.right - this.hitArea.left; } //dx = 正の値ならこのアクターが右側。相手の右端から、自分の左端を引いた値が重なりの幅。
if (dy < 0) { boundHeight = this.hitArea.bottom - other.top; } //dy = 負の値ならこのアクターが上側。自分の下端から、相手の上端を引いた値が重なりの高さ。
else if (dy > 0) { boundHeight = other.bottom - this.hitArea.top; } //dy = 正の値ならこのアクターが下側。相手の下端から、自分の上端を引いた値が重なりの高さ。
if (boundWidth <= boundHeight + 3) { // 横の重なりより縦の重なりが大きいなら、横の衝突。誤差3ピクセルまで許容
if (dx < 0) {
this._velocityX += -speed; // dx = 負の値ならこのアクターが左側。左にバウンス
if ( e.target.vector.dx < 0 ) { this._velocityX += e.target.vector.dx; } //相手が左側に移動してる時、その分を自分も移動
}
else if (dx > 0) {
this._velocityX += speed; // dx = 正の値ならこのアクターが右側。右にバウンス。
if ( e.target.vector.dx > 0 ) { this._velocityX += e.target.vector.dx; } //相手が右側に移動してる時、その分を自分も移動する。
}
}
if (boundHeight <= boundWidth + 3) { // 縦の重なりより横の重なりが大きいなら、縦の衝突。誤差3ピクセルまで許容
if (dy < 0) {
this._velocityY += -speed; // dy = 負の値ならこのアクターが上側、上にバウンス
if ( e.target.vector.dy < 0 ) { this._velocityY += e.target.vector.dy; } //相手が上側に移動してる時、その分を自分も移動する。
}
else if (dy > 0) {
this._velocityY += speed; // dy = 正の値ならこのアクターが下側、下にバウンス
if ( e.target.vector.dy > 0 ) { this._velocityY += e.target.vector.dy; } //相手が下側に移動してる時、その分を自分も移動する。
}
}
return;
}
矩形とのバウンスは、計算は単純なんですが...(各値の+か-かを比較して、条件分岐するだけ)
場合分けがかなり多くて、記述量が長くなってしまいます(o _ o。)
前回までの計算で、自分と相手の位置関係と、接触方向を比較。それによってバウンスの方向が求まりました。
ぶつかった時にバウンスする方向に対して、今回は追加で、相手の移動ベクトルも同じ方向かどうかを、X軸とY軸それぞれに対して比較してます。
もし反動ベクトルと方向が揃う場合、相手のXの移動値、Yの移動値をそのまま自分に反映させる感じです。
コードは長いくてこんがらがるケド、やってることは明確なんだ。。。
あああああああああああああああああプログラム言語ながなが。まさにとりーちゃん言語です。
とりーちゃん言語ですよ。こっこ・・・ 1or0,0or1,1010101,101111001010110101、模様。文字だけ見たらいみふめ。
相手が円形の場合の衝突判定式(相手の移動ベクトル含む)
if( other.type == 'circle') { //円形とのバウンス判定
const bounceVect = new Vector2D(this.hitArea.cx - other.cx, this.hitArea.cy - other.cy).normalVect; //相手の中心座標から自分の中心座標に向かうバウンス方向を単位ベクトルで求める
this._velocityX += speed * bounceVect.dx; //このアクターの速さに法線の単位ベクトルX軸をかけて反映
this._velocityY += speed * bounceVect.dy; //このアクターの速さに法線の単位ベクトルY軸をかけて反映
if ( e.target.vector.innerP(bounceVect) > 0 ) { //法線ベクトルと、相手の移動ベクトルの内積が正の値なら、相手の移動ベクトルも反映。
this._velocityX += e.target.vector.dx;
this._velocityY += e.target.vector.dy;
}
return;
}
円形だと、コードがすっきりして見やすい感じです。 追加部分はここです。
if ( e.target.vector.innerP(bounceVect) > 0 ) { //法線ベクトルと、相手の移動ベクトルの内積が正の値なら、相手の移動ベクトルも反映。
this._velocityX += e.target.vector.dx;
this._velocityY += e.target.vector.dy;
}
法線ベクトルと、相手の移動ベクトルを比較する際に、内積計算を利用してます。
(内積計算の詳細は、Lineクラスの項より。。。)
結果だけ見れば、内積の値が0より大きい正の値なら、ベクトル同士の角度が90度より小さい。方向がほぼ揃うので相手の移動ベクトルそのまま自分に反映させられる。
もし内積の値が0より小さい負の値なら、ベクトル同士の角度が90度より開いてしまう。方向が食い違うので、相手の移動ベクトルは無視されるという感じです。
(矩形の場合も、こういう描き方ならコードは短くて済むかもしれない...しかし今回は動作コストの軽い演算記法を優先しました。)
相手が線分(壁)の場合の衝突判定式(相手の移動ベクトル含む)
if( other.type=='line') { //壁、線分とのバウンス判定
const lineAB = e.target.hitArea; //ライン壁を定義
const delta = lineAB.crossAB(this.hitArea.cx, this.hitArea.cy); // このアクターは、ラインのどちら側に居るか?
let bounceVect; //法線ベクトル(衝突時の反動の方向)を定義する文字列。
if(e.target.isFall === true || delta > 0) { bounceVect = lineAB.bounceVect; } //deltaが正のとき、あるいは一方通行のとき、ラインの法線ベクトルを正でとる。
else { bounceVect = lineAB.bounceVect_; } //deltaが負のとき、ラインの法線ベクトルを負でとる。
if ( this.speed*this.speed < this.vector.length2 ) { speed = this.vector.length; } //もし自分の移動ベクトルが(押し戻しなどの影響で)自分の速度より大きくなってるなら、移動ベクトルの大きさを反動の大きさとする。
this._velocityX += speed * bounceVect.dx; //X軸の反動の大きさを反映
this._velocityY += speed * bounceVect.dy; //Y軸の反動の大きさを反映
//ここから衝突したライン側の移動ベクトルを反映させるかテスト
if ( e.target.vector.dx !== 0 || e.target.vector.dy !== 0 ) {//ラインの移動ベクトルが0ではないとき
const lineAP = new Line(e.target.hitArea.x, e.target.hitArea.y, this.hitArea.cx, this.hitArea.cy); //ラインの始点から自分の中心点に線を引く
const innerAX = lineAB.innerP(lineAP); //ラインの法線上に自分の中心点があるかどうか?に使う内積の値
if(0 <= innerAX && innerAX <= lineAB.length2) { // ラインの始点から終点までの法線上に、自分の中心点がある! 次の判定式へ
if ( e.target.vector.innerP(bounceVect) > 0 ) { // さらにラインの法線ベクトルと、ラインの移動ベクトルの内積が正の値なら、ラインの移動ベクトルも反映。
this._velocityX += e.target.vector.dx;
this._velocityY += e.target.vector.dy;
}
}
}
return;
}
さて、線分との衝突判定はちょっと難関です。もう一度、手順をおさらいします。
- ラインに対する自分の中心点の位置関係を調べる(ベクトルの外積計算を用いる。線の上か下か?)
- 線の上側なら、バウンス方向は法線ベクトルの正の値
- 線の下側なら、バウンス方向は法線ベクトルの負の値
- バウンス方向に、自分の速さ分だけ押し戻し
ここまでが、前回の押し戻し判定。
次に衝突相手の線分が移動してる場合を考える。
ここからは円形の場合と同じで...
- バウンス方向と、相手の移動ベクトルの方向関係を内積で調べる
- 内積が正なら、相手の移動ベクトルを自分に反映
- 内積が負なら、ベクトルがすれ違うので何もしない
これで、ライン相手の衝突判定が求まります...
が、いくつか意図しない挙動をする。。。
このLineクラスは、壁として扱うつもりで用意してます。
複数のアクターがぶつかって壁側にバウンスすることで、自分は立ち止まってるのに関わらず、壁にのめり込むケースが出てきてしまう...
というのを回避するために、壁相手の場合は、自分の前フレームの移動ベクトルの大きさも考慮に入れてます。
if ( this.speed*this.speed < this.vector.length2 ) { speed = this.vector.length; } //もし自分の移動ベクトルが(押し戻しなどの影響で)自分の速度より大きくなってるなら、移動ベクトルの大きさを反動の大きさとする。
もし自分の移動ベクトルが(押し戻しなどの影響で)自分の速度より大きくなってるなら、反動ベクトルの大きさは前フレームの移動距離とする。
これで、壁をすり抜けるバグは解消されました...たぶん。。。
それともう一点、問題が発生してました。
動く壁と衝突してから、壁を伝って(法線ベクトルと垂直に)移動した時に、衝突判定の範囲から外れたのに当たり判定が消えないバグ。なぜだ???
const lineAP = new Line(e.target.hitArea.x, e.target.hitArea.y, this.hitArea.cx, this.hitArea.cy); //ラインの始点から自分の中心点に線を引く
const innerAX = lineAB.innerP(lineAP); //ラインの法線上に自分の中心点があるかどうか?に使う内積の値
if(0 <= innerAX && innerAX <= lineAB.length2) { // ラインの始点から終点までの法線上に、自分の中心点がある! 次の判定式へ
とまぁ、動く壁相手にこんなことが起こったので、円と線分の衝突判定で用いた計算方法で、線分と中心点との最短距離が始点or終点となる場合、移動ベクトルを計算しないという式を加えました。
なぞ挙動すぎる... まぁこれで想定通りのバウンス判定が得られるようになりました。
超絶長い解説のわりに、あんま進んでない気がするのは何故だ。。。
あ、曲線との当たり判定とを平行してるお陰で、バウンス判定をしっかりやっとかねばという意識になりました。
バウンス処理、すっごい大切な要素でした。アクション要素はココ無くして何の応用もできん。
しかし記事書くのに1ヶ月以上もかかってる感じです。試行錯誤したので。長いので。。。ホント時間に余裕ないと難しいdすね。。焦ると何もならんし。うまくいく秘訣、1個ずつ堅実にやっていく他あるまい(o _ o。)
後日追記:バウンス処理の関数を外部化してまとめる
曲線の項まで描いた後日、このバウンス処理の関数はSpriteActorクラス内に直接書き込んでいましたが、100行近くにも及ぶため冗長になりすぎる。ということで、メンテナンス性を意識して、この部分を外部化することにしました。バウンス処理の関数を一つのクラスにまとめて追記。Actorクラスの外に外部化しておきます。
バウンスクラスの外部化
// このActorのhitAreaが矩形のときの、バウンス処理の関数をまとめたクラス。
class RectActorsBouncer {
detectCollision(actor, other, info) { //衝突判定時に、押し戻しの計算をする。相手の形状によって計算式を振り分ける。
if(other.hitArea.type==='rectangle') { return this.otherRectBounce(actor, other); } //矩形相手なら、矩形との反動ベクトルを
if(other.hitArea.type==='circle') { return this.otherCircleBounce(actor, other); } //円相手との反動ベクトルを
if(other.hitArea.type==='line') { return this.otherLineBounce(actor, other); } //線分との反動ベクトルを
if(other.hitArea.type==='bezierCurve' || other.hitArea.type==='quadraticCurve') { return this.otherCurveBounce(actor, other, info); } //曲線との反動ベクトルを
}
otherRectBounce(my, your) { //矩形相手とのバウンス処理
const dx = my.hitArea.cx - your.hitArea.cx; //お互いの中心座標(x軸)で位置関係を把握。正の値ならこのアクターが右側
const dy = my.hitArea.cy - your.hitArea.cy; //お互いの中心座標(y軸)で位置関係を把握。正の値ならこのアクターが下側
let speed = my.speed; //反動ベクトルの大きさを定義する。基本はこのアクターの速さ。
let boundWidth = 0, boundHeight = 0; //重なってる部分の幅と高さを定義
if (dx < 0) { boundWidth = my.hitArea.right - your.hitArea.left; } //dx = 負の値ならこのアクターが左側。自分の右端から、相手の左端を引いた値が重なりの幅。
else if (dx > 0) { boundWidth = your.hitArea.right - my.hitArea.left; } //dx = 正の値ならこのアクターが右側。相手の右端から、自分の左端を引いた値が重なりの幅。
if (dy < 0) { boundHeight = my.hitArea.bottom - your.hitArea.top; } //dy = 負の値ならこのアクターが上側。自分の下端から相手の上端を引いた値が重なりの高さ。
else if (dy > 0) { boundHeight = your.hitArea.bottom - my.hitArea.top; } //dy = 正の値ならこのアクターが下側。相手の下端から、自分の上端を引いた値が重なりの高さ。
if (boundWidth <= boundHeight + 3) { // 横の重なりより縦の重なりが大きいなら、横の衝突。誤差3ピクセルまで許容
if (dx < 0) { my._velocityX += -speed; // dx = 負の値ならこのアクターが左側。左にバウンス
if ( your.vector.dx < 0 ) { my._velocityX += your.vector.dx; } //相手が左側に移動してる時、その分を自分も移動する。
}
else if (dx > 0) { my._velocityX += speed; // dx = 正の値ならこのアクターが右側。右にバウンス。
if ( your.vector.dx > 0 ) { my._velocityX += your.vector.dx; } //相手が右側に移動してる時、その分を自分も移動する。
}
}
if (boundHeight <= boundWidth + 3) { // 縦の重なりより横の重なりが大きいなら、縦の衝突。誤差3ピクセルまで許容
if (dy < 0) { my._velocityY += -speed; // dy = 負の値ならこのアクターが上側、上にバウンス
if ( your.vector.dy < 0 ) { my._velocityY += your.vector.dy; } //相手が上側に移動してる時、その分を自分も移動する。
}
else if (dy > 0) { my._velocityY += speed; // dy = 正の値ならこのアクターが下側、下にバウンス
if ( your.vector.dy > 0 ) { my._velocityY += your.vector.dy; } //相手が下側に移動してる時、その分を自分も移動する。
}
}
}
otherCircleBounce(my, circle) { //円形相手とのバウンス処理
let speed = my.speed; //反動ベクトルの大きさを定義する。基本はこのアクターの速さ。
const bounceVect = new Vector2D(my.hitArea.cx - circle.hitArea.cx, my.hitArea.cy - circle.hitArea.cy).normalVect; //相手の中心座標から自分の中心座標に向かうバウンス方向を単位ベクトルで求める
my._velocityX += speed * bounceVect.dx; //このアクターの速さに法線の単位ベクトルX軸をかけて反映
my._velocityY += speed * bounceVect.dy; //このアクターの速さに法線の単位ベクトルY軸をかけて反映
if ( circle.vector.innerP(bounceVect) > 0 ) { //法線ベクトルと、相手の移動ベクトルの内積が正の値なら、相手の移動ベクトルも反映。
my._velocityX += circle.vector.dx;
my._velocityY += circle.vector.dy;
}
}
otherLineBounce(my, line) { //線分相手とのバウンス処理
let speed = my.speed; //反動ベクトルの大きさを定義する。基本はこのアクターの速さ。
const lineAB = line.hitArea; //ライン壁を定義
const delta = lineAB.crossAB(my.hitArea.cx, my.hitArea.cy); // このアクターは、ラインのどちら側に居るか?
const bounceVect = lineAB.bounceVect; //法線ベクトル(衝突時の反動の方向)を定義する文字列。
if (!line.isFall && delta < 0) { bounceVect.dx*=-1; bounceVect.dy*=-1; } //壁が一方通行でない&&deltaが負のとき、ラインの法線ベクトルを負でとる。
if ( speed*speed < my.vector.length2 ) { speed = my.vector.length; } //もし自分の移動ベクトルが(押し戻しなどの影響で)自分の速度より大きくなってるなら、移動ベクトルの大きさを反動の大きさとする。
my._velocityX += speed * bounceVect.dx; //X軸の反動の大きさを反映
my._velocityY += speed * bounceVect.dy; //Y軸の反動の大きさを反映
//ここから衝突したライン側の移動ベクトルを反映させるかテスト
if ( line.vector.dx !== 0 || line.vector.dy !== 0 ) {//ラインの移動ベクトルが0ではないとき
const innerAX = lineAB.innerAB(my.hitArea.cx, my.hitArea.cy); //ラインの法線上に自分の中心点があるかどうか?に使う内積の値
if(0 <= innerAX && innerAX <= lineAB.length2) { // ラインの始点から終点までの法線上に、自分の中心点がある! 次の判定式へ
if ( line.vector.innerP(bounceVect) > 0 ) { // さらにラインの法線ベクトルと、ラインの移動ベクトルの内積が正の値なら、ラインの移動ベクトルも反映。
my._velocityX += line.vector.dx;
my._velocityY += line.vector.dy;
}
}
}
}
otherCurveBounce(my, curve, info) { //曲線相手とのバウンス処理
let speed = my.speed; //反動ベクトルの大きさを定義する。基本はこのアクターの速さ。
const tSum = info.reduce((a, c) => a + c); // 交点となるtの解の和(複数の場合)
const t = tSum / info.length; // tの解の平均値を得る、このtから法線ベクトルを求める
//const otherCx = curve.hitArea.fx(t), otherCy = curve.hitArea.fy(t); 曲線上のバウンドの起点となるXとYの座標を求める
const delta = new Vector2D (my.hitArea.cx - curve.hitArea.fx(t), my.hitArea.cy - curve.hitArea.fy(t)); //曲線上のバウンドの起点から自分の中心点までのベクトルで、お互いの位置関係を取得
const bounceVect = curve.hitArea.bounceVect(t).normalVect; // 法線の単位ベクトルを取得する(バウンド方向)
if(bounceVect.innerP(delta) < 0 && !curve.isFall) {bounceVect.dx*=-1; bounceVect.dy*=-1;} // もし法線が逆さ(内積が負)なら、ベクトルを逆向きにする。
if ( speed*speed < my.vector.length2 ) { speed = my.vector.length; } //もし自分の移動ベクトルが(押し戻しなどの影響で)自分の速度より大きくなってるなら、移動ベクトルの大きさを反動の大きさとする。*/
my._velocityX += speed * bounceVect.dx *1.0625; //X軸の反動の大きさを反映 乗り越えを防ぐのに、反動の大きさ1/16増し。
my._velocityY += speed * bounceVect.dy *1.0625; //Y軸の反動の大きさを反映
}
}
SpriteActorの要素内にバウンスクラスを定義して呼びこむ
class SpriteActor extends Actor {//影描画を当てはめた基本のSpriteActor
constructor(x, y, sprite, hitArea, tags=[]) {
super(x, y, hitArea, tags);
this.sprite = sprite;//画像
this._dir = 270; //アクターの向き...deg表記で。
this._velocityX = 0; //フレーム中のx軸の移動値
this._velocityY = 0; //フレーム中のy軸の移動値
this.isHit = 0; // hit中かどうか
this.isStand = true; //立ち止まってる状態かどうか
this.isDash = false; // ダッシュ中かどうか
this.walkSpeed = 2; //歩くスピード
this.walkCount = 0; // 移動距離のカウント
this.bouncer = new RectActorsBouncer(); // ここを追加
this.addEventListener('hit', (e) => { //当たり判定発生時のバウンス判定
if(!e.target.hasTag('playerAction') && !e.target.hasTag('event') && !e.target.hasTag('floar') && !e.target.hasTag('element')) { //これらのタグ相手とはバウンス判定しない。
if( this.isHit < 12 ) { this.isHit = 12; }
this.bouncer.detectCollision(this, e.target, e.info); //ここで関数を使用
}
});
}
そしてSpriteActorの方ではこの関数のクラスを要素に定義し、必要なときに読みこめば記述を1行で省略できるようになります。
スッキリと見通しが良くなりましたし、Actorの形状が変わる際にもそれ用の関数に置き換えれば良いだけなので、メンテナンスも楽になると思います。
次回、いよいよ二次曲線という形状の当たり判定に挑戦。。(難度が跳ね上がるので飛ばしても良い)
⇒ JavaScriptでゲーム作り「10EX:2次曲線の当たり判定とバウンス処理」
すぺしゃるさんくす
古都さんのフレームワークを元にほぼ最初から作ってます。
たぶん順番に見ないとちんぷんかんぷん(' '*)...
https://sbfl.net/
古都さん
JavaScriptで作る弾幕STGの基礎(フレームワーク)を使わせていただいてます。感謝!

ぴぽやさんもありがとう、キャラチップをお借りしています。