12:キャッシュの扱い方と計算処理の高速化
前回8項にて、計算処理の工夫をいくつかメモしました。。今回はそれの続きです。主にキャッシュ部分(計算途中の一時保存データ)の扱い方やget/set関数による調製例、シフト演算処理などについて見ていきたいと思います。ちょっとした記述の差で速度が段違いに変わる
(2019.5.03執筆)
何と言っても、まず無駄な計算量を無くしていくことが肝心でしょうか。矩形アクター50個、円形50個、3次曲線2つに線分2つ、矩形のキャラが2人で当たり判定の速度テストしてみてます。
従来の速度
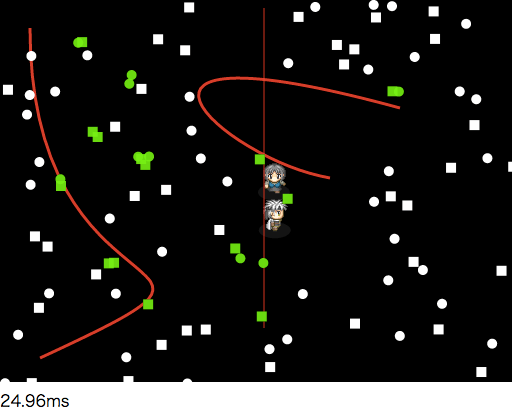
改善後の速度
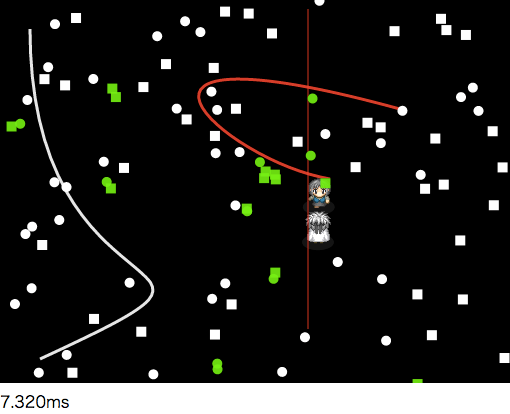
改善後は約1/3にまで軽減された。順に改善例を見ていきます。
- 処理の重い計算(関数)は、毎回呼び出すのではなく計算結果を保存しておいて、その値を読み込むようにする
- ↑ 一時保存データ(キャッシュ)の扱い方と注意点
- 毎回呼び出す関数の条件分岐は、できるだけ最小限で済むように
- 無駄なキャッシュをさせない。関数に渡す必要な値は最小限に
こんな感じでしょうか...(' '*)
キャッシュを活用する
処理の重い計算(関数)...例えば塁乗とか割り算とか√計算とか非常に重たいのですが、こういったのは毎回呼び出すのではなく最初の段階で計算結果を保存しておいて、使う際にその値を読み込むようにすると高速化します。計算処理を省略できるからですね。これがキャッシュ(一時保存データ)の活用と呼ばれるみたいです。例えば円の当たり判定をとるのに、円の中心点から対象の点までの距離を3平方の定理で測り、半径の長さと比較する方法がありますが。
例:円と対象の座標点が接するかどうかの判定式
circle.radius**2 >= point.x**2 + point.y**2円の中心点を(0,0)の原点基準にした時の、対象の座標点との距離を半径と比較する計算式です。半径以内ならその点と接触判定。
厳密には√計算を用いて、半径の長さ >= √(x座標の2乗 + y座標の2乗)...なのですが、比較演算式なので両辺を2乗した値でも計算できます。√計算を使わない方が計算早いのでこちらで。 しかしこの場合も、当たり判定を計算する度に半径を毎回2乗する必要があります。たかだか2乗ですが、それが何十回何百回となると、なかなか大変ですね。
そこで円形クラスの要素内に、半径を2乗した値を予め保存しておく工夫をします。
円形クラス(Collider)の改善例
class Circle extends Collider { //当たり判定を円形で使うクラス
constructor(x, y, radius) { //中心点(x,y)の座標と、半径radiusを持つ円の定義
super('circle', x, y);
this.radius = radius;
this.radius2 = this.radius*this.radius; // 半径の2乗の値を格納。距離計算に使う
}
get cx() { return this.x; } //円の中心のX座標、矩形と同様にcxでも取得できるように
get cy() { return this.y; } //円の中心のY座標、矩形と同様にcyでも取得できるように
get top() { return this.y - this.radius; } // 四分木の空間登録で使う
get bottom() { return this.y + this.radius; } // 同上
get left() { return this.x - this.radius; } // 同上
get right() { return this.x + this.radius; } // 同上
}
this.radius2に、半径を2乗した値を定め、いつでも読み込める状態になりました。
これによって、円と点との接触判定式が簡略化されます。改善後:円と対象の座標点が接するかどうかの判定式
circle.radius2 >= point.x**2 + point.y**2
単純に累乗計算量が2/3になったので、少し処理も高速化されたと思います。
キャッシュの注意点「計算した値を変更しなくてはならない場合」
キャッシュの利点は計算処理を削減できる点で素晴らしいのですが、一度計算した値を変更しなくてはならない場合の対処が苦手です。 例えば上記の例だと、円の半径が変わってしまうと2乗の値も変わらなければいけませんが、記述がそのままだと変更前の状態でずっと続いてしまいます。
class Circle extends Collider { //当たり判定を円形で使うクラス
this.radius = radius; //途中で変化させない
this.radius2 = this.radius*this.radius; // この値は固定されたまま
}
キャッシュに格納するなら、もうその値は変更をしない!と割りきって使うと潔いです。いい感じです。
。。。(' '*)
しかしどうしても値を変化させたいしキャッシュも活用したい場合、get/set()関数を同時活用するといった方法があります。
get/set()関数を使って、関連したキャッシュの値も変更させる
class Circle extends Collider { //当たり判定を円形で使うクラス
constructor(x, y, radius) { //中心点(x,y)の座標と、半径radiusを持つ円の定義
super('circle', x, y);
this.radius = radius;
}
get radius() { return this._radius; }
set radius(value) { this._radius = value; this.radius2 = value*value; } // 半径の値が代入された時、半径の2乗の値も格納
}
get/setを組み合わせると、特定の値を変更した際に合わせて、別の関数を実行させることができます。今回は半径の2乗の値を更新させるようにしました。このようにすると、2乗計算のキャッシュも更新してくれるようになります。しかし値の更新が必要じゃない場面で、不必要な2乗計算をしてしまいかねないという面も持ち合わせます。キャッシュの計算はそれが重たいほど効果が高まりますが、変更回数が多いと逆に負担が増える。そのことも踏まえて、キャッシュを更新するためにsetを活用するのは最小限に留めることを心に入れておいたほうが良いかもしれません。
値が必要になったら初めて計算。次回以降はキャッシュから呼び出す
最初に必要な値を計算してキャッシュするのもいいですが、それが必ずしも必要でないこともあります。 例えば、2点間を結ぶ線分の長さの値。。。例:線分の長さを求める計算式
line.length = Math.sqrt(line.dx**2 + line.dy**2);
累乗計算が2回に、√計算が1回の手順。かなり重たいコストです。 この値はバウンス処理のとき、この線分の法線だったり単位ベクトルを求めたりするのにどうしても必要になってきます。
しかし単純な当たり判定には、距離の2乗計算...つまり
線分の長さの2乗を求める計算式
line.length2 = line.dx**2 + line.dy**2
距離の2乗した値さえあれば当たり判定は事足りる(矩形との判定なら距離の2乗計算すら要らない場合もある)ので、必ずしも線分の長さが必要なわけでもありません。 そこでクラス生成時は要素を空にしておいて、初めて必要になった時に計算式を呼び出す。以降、その計算結果を保存したのを呼び出す。というような工夫も考えられます。
線分クラス(Collider)の改善例
class Line extends Collider { //当たり判定を線で扱うクラス 背景オブジェクトの通行判定に使う予定
constructor(x, y, x1, y1) {
super('line', x, y);
this.x1 = x1; //終着点のx座標
this.y1 = y1; //終着点のy座標
this._length = null; //この線分の長さを格納、初期値は空
this._length2 = null; //この線分の長さの2乗を格納、初期値は空
}
get dx() { return this.x1 - this.x; } // x軸の移動方向と距離を求める、ベクトル成分のxになる
get dy() { return this.y1 - this.y; } // y軸の移動方向と距離を求める、ベクトル成分のyになる
get length() { return this._length = this._length || Math.sqrt(this.length2); } // この線分の長さを格納しながら計算結果を返す。以降、値を即呼び出せる。
get length2() { return this._length2 = this._length2 || this.dx * this.dx + this.dy * this.dy; } // 長さの2乗(距離の比較など、√計算省略で活用
}
えっと、get length(){}という部分がそうで、値が入ってる状態ならそのまま。もし存在しない場合は計算式を呼び出して計算する感じです。この描き方をすると、必要になった時に初めて値が計算されるので使い勝手が良さそうです。
あ、先ほどの円の半径の2乗を求める関数も、こういった記述法だと良さそうですね。
円形クラス(collider)のさらに改善例
class Circle extends Collider { //当たり判定を円形で使うクラス
constructor(x, y, radius) { //中心点(x,y)の座標と、半径radiusを持つ円の定義
super('circle', x, y);
this.radius = radius;
}
get radius() { return this._radius; }
set radius(value) { this._radius = value; this._radius2 = null; } // 半径の値が代入された時、半径の2乗の値を初期化
get radius2() { return this._radius2 = this._radius2 || this._radius*this._radius; } //半径の2乗の値を計算、2回目以降は計算結果を呼び出すだけ
}
このset関数だと、半径の値を変化させても2乗の値は初期化(null)するだけなので処理は軽いです。 必要なときにget radius2()で計算式を呼び出して、nullでなければ値をそのまま、それ以外ならもう一度計算しなおして値を返す。といった感じ。
get/setの良いところを両立できて、なかなか使い勝手が良さそうです。これで行きましょう。
ただし、コードが読みづらくなる所は微妙かも。。(o _ o。)
関数内のconst(変数)を上手に使う
キャッシュの活用は、値をオブジェクト要素に格納するだけではありません。関数内に定義するconstの変数も、一時的に同じ役割を果たします(関数を抜けると役目を終えます)...例 2次曲線と線分の交差判定に使う2次方程式の解の公式
//解の公式を使うために、a*t*t + 2*b*t + c = 0;の形に整理し、定数a,b,cの値を定義する。
const a = line.dy* qCurve.d2x - line.dx* qCurve.d2y;
const b = line.dy* qCurve.dx - line.dx* qCurve.dy;
const c = line.dy* qCurve.x - line.dx* qCurve.y + line.dx*line.y - line.dy*line.x;
//解の公式Ⅱ t = (-b ± Math.sqrt(b*b - a*c))/a
//解の公式Ⅱを用いて2次方程式の定数tの値(2つある)を得る判定
const delta = b*b - a*c; //Math.sqrt(b*b - a*c))の中身を判定
const timeCurveCheck = []; //求めたtの解をチェックする配列
if (delta < 0) {return false;} //delta が負に値になるとき、解はない。交点が存在しない
else if (delta === 0) { //delta=0 のとき、tの解は1つ。timeCurveCheckリストにtの解を一つ追加する
timeCurveCheck.push( -b/a ); //tの解 = -b/a
}
else if (delta > 0) { //delta>0 のとき、tの解は2つ。timeCurveCheckリストにtの解を二つ追加する
const sqrtDelta = Math.sqrt(delta);
timeCurveCheck.push( (-b + sqrtDelta)/a ); //tの解1つめ = -b + Math.sqrt(delta))/a
timeCurveCheck.push( (-b - sqrtDelta)/a ); //tの解2つめ = -b - Math.sqrt(delta))/a
}
ここでのポイントは、2次方程式の解の公式Ⅱで使う解 = (-b ± Math.sqrt(b*b - a*c))/a ...の判定の順番です。 まず± Math.sqrt(b*b - a*c)の中身...const delta = b*b - a*c;の値を定義して、条件分けしてます。以降deltaの値は計算せずに使いまわせる。
この値が負に傾くなら、そもそも解が存在しないことになるので√計算するまでもなくfalseをreturnできる。 この値が0なら、解は-b/aでreturnできる・・・ もし値>0なら解が2つ存在しますが、そこでconst sqrtDelta = Math.sqrt(delta);と√計算をしたものを定義すれば、最大でも√計算は1回で済むようになります。
constの定義も上手く使うと、計算の手間を最小限に抑えることができる感じです。
関数の条件分岐は、できるだけ最小限で済むように
次に条件分岐について。案外、if()を使った条件分岐というのもタダじゃないようです。if()の回数が少なければ少ないほど関数の処理は早くなる。例:従来の当たり判定での形状振り分け式
detectCollision(c1, c2) { //シーンにて、各ActorのhitArea同士で、この当たり判定式を呼び出している
if(c1.type == 'rectangle' && c2.type=='rectangle') { return this.deRectRect(c1, c2); } //矩形なら、矩形同士の衝突判定式を
if(c1.type == 'rectangle' && c2.type=='circle') { return this.deRectCircle(c1, c2); } //矩形と円同士の衝突判定式を
if(c1.type == 'circle' && c2.type=='rectangle') { return this.deRectCircle(c2, c1); } //円と矩形同士の衝突判定式を
if(c1.type == 'circle' && c2.type=='circle') { return this.deCircleCircle(c1, c2); } //円なら、円同士の衝突判定式を
if(c1.type == 'rectangle' && c2.type=='line') { return this.deRectLine(c1, c2); } //矩形と線分同士の衝突判定式を
if(c1.type == 'line' && c2.type=='rectangle') { return this.deRectLine(c2, c1); } //線分と矩形同士の衝突判定式を
if(c1.type == 'circle' && c2.type=='line') { return this.deCircleLine(c1, c2); } //円と線分同士の衝突判定式を
if(c1.type == 'line' && c2.type=='circle') { return this.deCircleLine(c2, c1); } //線分と円同士の衝突判定式を
if(c1.type == 'line' && c2.type=='line') { return this.deLineLine(c1, c2); } //線分と円同士の衝突判定式を
if(c1.type == 'rectangle' && c2.type=='bezierCurve') { return this.deRectBezierCurve(c1, c2); } //矩形と3次ベジェ曲線の衝突判定式を
if(c1.type == 'bezierCurve' && c2.type=='rectangle') { return this.deRectBezierCurve(c2, c1); } //3次ベジェ曲線と矩形の衝突判定式を
if(c1.type == 'line' && c2.type=='quadraticCurve') { return this.deLineQCurve(c1, c2); } //線分と2次ベジェ曲線の衝突判定式を
if(c1.type == 'quadraticCurve' && c2.type=='line') { return this.deLineQCurve(c2, c1); } //2次ベジェ曲線と線分の衝突判定式を
if(c1.type == 'rectangle' && c2.type=='quadraticCurve') { return this.deRectQCurve(c1, c2); } //矩形と2次ベジェ曲線の衝突判定式を
if(c1.type == 'quadraticCurve' && c2.type=='rectangle') { return this.deRectQCurve(c2, c1); } //2次ベジェ曲線と矩形の衝突判定式を
return false; //形状の種類が多くなるほど判定式を選ぶのに遅くなる。なるだけ多用する形状順に判定式を記述。
}
....(' '*) でたらめに長いですよね。なにせ矩形と円形と線分と2次曲線と3次曲線の5種類が総当り。これじゃ無駄も多い。
例の改善後;当たり判定での形状振り分け式
detectCollision(c1, c2) { //シーンにて、各ActorのhitArea同士で、この当たり判定式を呼び出している
if(!this.hitRectRect(c1.aabbRect, c2.aabbRect)) {return false;} // 形状に関わらず、最初にaabbの矩形範囲で判定。falseなら当たってない判定で終了
else if(c1.type === 'rectangle') { //c1が矩形の場合
if(c2.type==='rectangle') { return true; } //矩形なら、矩形同士のaabb衝突判定式すでにtrue
else if(c2.type==='bezierCurve') { return this.hitRectBezierCurve(c1, c2); } //矩形と3次ベジェ曲線の衝突判定式を
else if(c2.type==='line') { return this.hitRectLine(c1, c2); } //矩形と線分同士の衝突判定式を
else if(c2.type==='circle') { return this.hitRectCircle(c1, c2); } //矩形と円同士の衝突判定式を
else if(c2.type==='polygon') { return this.hitRectPolygon(c1, c2); } //矩形と多角形同士の衝突判定式を
}
else if(c1.type === 'bezierCurve') { //c1が3次ベジェ曲線の場合
if(c2.type==='rectangle') { return this.hitRectBezierCurve(c2, c1); } //3次ベジェ曲線と矩形の衝突判定式を
}
else if(c1.type === 'line') { //c1が線分の場合
if(c2.type==='rectangle') { return this.hitRectLine(c2, c1); } //線分と矩形同士の衝突判定式を
if(c2.type==='line') { return this.hitLineLine(c1, c2); } //線分と円同士の衝突判定式を
if(c2.type==='circle') { return this.hitCircleLine(c2, c1); } //線分と円同士の衝突判定式を
}
else if(c1.type === 'circle') { //c1が円形の場合
if(c2.type==='rectangle') { return this.hitRectCircle(c2, c1); } //円と矩形同士の衝突判定式を
if(c2.type==='circle') { return this.hitCircleCircle(c1, c2); } //円なら、円同士の衝突判定式を
if(c2.type==='line') { return this.hitCircleLine(c1, c2); } //円と線分同士の衝突判定式を
}
else if(c1.type === 'polygon') { //c1が多角形の場合
if(c2.type==='rectangle') { return this.hitRectPolygon(c2, c1); } //多角形と矩形の衝突判定式を
}
}
改善後。5種類の形状を振り分けてますが、1形状ずつ段階を踏んでるのでif()のステップも短くて済んでます。
最初にaabb矩形での判定
if(!this.hitRectRect(c1.aabbRect, c2.aabbRect)) {return false;} // 形状に関わらず、最初にaabbの矩形範囲で判定。falseなら当たってない判定で終了
何と言っても最大の効果があったのがこの一行です。形状に関わらず、最初にaabbの矩形範囲で判定。falseなら当たってない判定で終了。これによって、範囲外のオブジェクトならどんな形状であれ1回でfalse判定を出せるようになってます。つまり円形とか多角形とかも、範囲外オブジェクトなら矩形(一番軽い形状)とほぼ同コストで扱えるように。
無駄なキャッシュをさせない。関数に渡す必要な値は最小限に
aabb矩形同士の判定式にも改善点がありました。矩形同士の衝突判定式を確認する
hitRectRect(rect1, rect2) { //矩形同士の衝突判定式
const horizontal = (rect2.left < rect1.right) && (rect1.left < rect2.right); //水平方向の距離
const vertical = (rect2.top < rect1.bottom) && (rect1.top < rect2.bottom); //垂直方向の距離
return (horizontal && vertical); //両方の条件が一致すれば接触判定
}
これは矩形同士の衝突判定式ですが、aabb矩形でもこの判定を使っています。 関数内にはrectが渡されてますが、計算に使うのはrectオブジェクト内のleft,right,top,bottomの4つの要素です。
従来のaabb矩形を求める関数を見直す
get aabbRect() { // この形状の範囲を表すaabb矩形
const width = this.right - this.left;
const height = this.bottom - this.top;
return new Rectangle( this.left, this.top, width, height);
}
ここで、従来のaabb矩形を求める関数を見なおしてみますと...何と、せっかく4隅の値が求まっているのに関わらず、矩形クラスに合わせてwidth幅とheight高さの値を計算して結果を返しています。
当たり判定に使う元の矩形クラス
class Rectangle extends Collider { //当たり判定を四角形で使うクラス
constructor(x, y, width, height) {
super('rectangle', x, y);
this.width = width;
this.height = height;
}
get cx() { return this.x + this.width*0.5; } //矩形の中心のX座標
get cy() { return this.y + this.height*0.5; } //矩形の中心のY座標
get top() { return this.y; }
get bottom() { return this.y + this.height; }
get left() { return this.x; }
get right() { return this.x + this.width; }
get aabbRect() { return this; } //hitTestで最初のaabb判定に使う。各形状共通のメソッド
}
しかも矩形クラスを見なおせば、この後のaabb衝突判定で幅と高さからrightとbottomの値を計算し直す二重の手間が... これ何百回と重なったら相当なものです。特に3次曲線クラスではaabb矩形の判定を多用するので尚更。
aabb矩形専用のクラスを用意
class aabbRect { //hitTestの最初にaabbで判定を取るためのクラス
constructor(left, top, right, bottom) {
this.left = left;
this.top = top;
this.right = right;
this.bottom = bottom;
}
}
なのでaabb矩形の4隅へ直にアクセスできる専用クラスを用意しました。このaabbクラスは現フレームのaabb接触判定で役目を終えます。だから最小限でいい。改善後のaabb矩形を求める関数
get aabbRect() { return new aabbRect(this.left, this.top, this.right, this.bottom); } //hitTestで最初のaabb判定に使う。各形状共通のメソッド
この記述と併用して形状分岐の前にaabbの判定を設けたら、速度が大幅に改善されました。足し算引き算が必要なくなっただけで目に見える効果です(' '*)...ちなみにFirefoxで試してますが、Chromeの方は最初から最適化がなされてるのか、違いは微々たるものでした。(それでも改善効果は多少ありました)
関数内で繰り返し呼び出すクラスならば、必要な値のみを抜き出した最小限のクラスで渡すのが好感触でした。
基礎編ここまでとなります。参考成るかわからんけど読んでくれてありがとう(' '*)
この下に続いてる文は読み飛ばしOKです。
キャッシュの活用例:3次曲線クラスの計算高速化
class BezierCurve extends Collider { //当たり判定を3次曲線で扱うクラス。地形を現す曲線なのでマップに固定。通行判定に使う予定。
constructor(x, y, x1, y1, x2, y2, x3, y3, divLevel=5) {
super('bezierCurve', x, y);
this.x1 = x1; //制御点1のx座標
this.y1 = y1; //制御点1のy座標
this.x2 = x2; //制御点2のx座標
this.y2 = y2; //制御点2のy座標
this.x3 = x3; //終着点のx座標
this.y3 = y3; //終着点のy座標
this.d3x = this.x3 - this.x + 3*(this.x1 - this.x2); // fx(t) t**3の係数
this.d2x = this.x2 - 2*this.x1 + this.x; // fx(t) t**2の係数の1/3...使う時は3*d2xとして使う。
this.dx = this.x1 - this.x; // fx(t) t**1の係数の1/3...使う時は3*dxとして使う。
this.d3y = this.y3 - this.y + 3*(this.y1 - this.y2); // fy(t) t**3の係数
this.d2y = this.y2 - 2*this.y1 + this.y; // fy(t) t**2の係数の1/3...使う時は3*d2yとして使う。
this.dy = this.y1 - this.y; // fy(t) t**1の係数の1/3...使う時は3*dyとして使う。
// X,Yそれぞれが極値となるt値を格納。値は最大2つずつ存在
this.xLimT = [];
this.yLimT = [];
// X,Yの極値となるt値を求める
this.xLimTcheck();
this.yLimTcheck();
// 求めたtの配列から、X,Yの極値の座標を配列に格納する
this.XnoKIWAMI = this.xLimT.map( (t) => this.fx(t) );
this.YnoKIWAMI = this.yLimT.map( (t) => this.fy(t) );
// 曲線を指定した値で分割して、その地点の座標を配列に格納する。初期値は32分割
this.divNumber = 1 << divLevel; // = Math.pow(2, divLevel); // 曲線判定の分割数は、2のn乗とする n=分割レベル。初期値は32分割となるよう調整
this.clipT = 1 / this.divNumber; // 配列のインデックス値iからtの値を求めるのに使う i*clipT = t
// 求めたtの極値から、配列のインデックス番号と比較できる値を求める *this.divNumber
this.X_LimIndex = this.xLimT.map( (t) => t *this.divNumber );
this.Y_LimIndex = this.yLimT.map( (t) => t *this.divNumber );
this.tArray = this.tArray(this.divNumber); //tをn分割した座標の配列...this.tArray[0] => {x:fx(0), y:fy(0)}
const yMinMax = this.yMinMax(0, this.divNumber);
const xMinMax = this.xMinMax(0, this.divNumber);
// 曲線のAABB矩形を囲む4隅の座標を保存する要素
this.top = yMinMax.min; //tが0〜1の間のyの最小値が上端
this.bottom = yMinMax.max; //tが0〜1の間のyの最大値が下端
this.left = xMinMax.min; //tが0〜1の間のxの最小値が左端
this.right = xMinMax.max; //tが0〜1の間のxの最大値が右端
}
/* 3次ベジェ曲線の数式(0 <= t <=1) t地点の座標を求める*/
fx(t) { return this.d3x*t*t*t + 3*this.d2x*t*t + 3*this.dx*t + this.x; } //tを代入してX座標取得
fy(t) { return this.d3y*t*t*t + 3*this.d2y*t*t + 3*this.dy*t + this.y; } //tを代入してY座標取得
/*3次ベジェ曲線の微分式(0 <= t <=1) t地点の傾きを調べる*/
f1x(t) { return 3*(this.d3x*t*t + 2*this.d2x*t + this.dx);}
f1y(t) { return 3*(this.d3y*t*t + 2*this.d2y*t + this.dy);}
bounceVect(t) { // tのときの曲線上の微分式から法線ベクトルを求める
const dx = this.f1x(t), dy = this.f1y(t);
return new Vector2D(-dy, dx); // 曲線のt地点における傾きに垂直なベクトルを返す
}
xLimTcheck() { // Xの極値となるt値を求める
const delta = this.d2x*this.d2x - this.d3x*this.dx;
if( delta <= 0 ) { return; }//微分式=0のtが虚数解になるならYの極値tは無い
else { const sqrtDelta = Math.sqrt(delta); // 解の公式より、2つの解が求まる。
const tCheck = []; // 求めたtの解が0〜1の間のみ条件を満たす
tCheck.push( (-this.d2x + sqrtDelta)/this.d3x );
tCheck.push( (-this.d2x - sqrtDelta)/this.d3x );
for(let t of tCheck) {
if(0 < t && t < 1) { this.xLimT.push(t); }
}
this.xLimT.sort( (a,c) => a-c ); // tの配列を昇順に
}
}
yLimTcheck() { // Yの極値となるt値を求める
const delta = this.d2y*this.d2y - this.d3y*this.dy;
if( delta <= 0 ) { return; }//微分式=0のtが虚数解になるならYの極値tは無い
else { const sqrtDelta = Math.sqrt(delta); // 解の公式より、2つの解が求まる。
const tCheck = []; // 求めたtの解が0〜1の間のみ条件を満たす
tCheck.push( (-this.d2y + sqrtDelta)/this.d3y );
tCheck.push( (-this.d2y - sqrtDelta)/this.d3y );
for(let t of tCheck) {
if(0 < t && t < 1) {this.yLimT.push(t); }
}
this.yLimT.sort( (a,c) => a-c ); // tの配列を昇順に
}
}
tArray(divNumber) { // 曲線上のtをdivNumberだけ分割した、それぞれの座標を配列でreturnする
const tArray = [];
for (let i=0; i <= divNumber; i++) {
const t = i * this.clipT;
tArray.push( {x:this.fx(t), y:this.fy(t)} );
}
return tArray;
}
yMinMax(i0, i1) { /* tがt0〜t1における範囲の、yの最大最小を求める(初期値は0 <= t <=1 にthis.divNumberをかけた値*/
//const i0 = t0*this.divNumber, i1 = t1*this.divNumber; // tに曲線の分割数を掛ける、これが曲線を分割した座標の配列にアクセスできるインデックス値になる
const yCheck = [this.tArray[i0].y, this.tArray[i1].y]; // 両端のy座標を配列から取り出し、チェックリストに追加
for (let i=0; i < this.Y_LimIndex.length; i++) { // 極値となるtが範囲内か順番に確認
if( i1 <= this.Y_LimIndex[i] ) { return { min:Math.min(...yCheck), max:Math.max(...yCheck) }; } // 昇順なので、すでに大きい場合はこの時点で結果をreturnできる
if( i0 < this.Y_LimIndex[i] ) { yCheck.push(this.YnoKIWAMI[i]); } // もし極値となるtが範囲内なら、極値の座標もチェックリストに加える
}
return { min:Math.min(...yCheck), max:Math.max(...yCheck) }; // 範囲内のyの最小値と最大値を返す
}
xMinMax(i0, i1) { /* tがt0〜t1における範囲の、xの最大最小を求める(初期値は0 <= t <=1 にthis.divNumberをかけた値*/
//const i0 = t0*this.divNumber, i1 = t1*this.divNumber; // tに曲線の分割数を掛ける、これが曲線を分割した座標の配列にアクセスできるインデックス値になる
const xCheck = [this.tArray[i0].x, this.tArray[i1].x]; // 両端のy座標を配列から取り出し、チェックリストに追加
for (let i=0; i < this.X_LimIndex.length; i++) { // 極値となるtが範囲内か順番に確認
if( i1 <= this.X_LimIndex[i] ) { return { min:Math.min(...xCheck), max:Math.max(...xCheck) }; } // 昇順なので、すでに大きい場合はこの時点で結果をreturnできる
if( i0 < this.X_LimIndex[i] ) { xCheck.push(this.XnoKIWAMI[i]); } // もし極値となるtが範囲内なら、極値の座標もチェックリストに加える
}
return { min:Math.min(...xCheck), max:Math.max(...xCheck) }; // 範囲内のxの最小値と最大値を返す
}
get aabbRect() { // 曲線と接するaabb矩形
return new aabbRect( this.left, this.top, this.right, this.bottom);
}
aabbRect2(i0, i1) { //t0*this.divNumber〜t1*this.divNumberの区間で分割した曲線のaabb矩形
const xLim = this.xMinMax(i0, i1), yLim = this.yMinMax(i0, i1);
return new aabbRect( xLim.min, yLim.min, xLim.max, yLim.max );
}
}
さて、唐突に3次曲線についての話題になりますが、こいつは円や線分とは比べ物にならないほどの計算量を必要とします。正直、ゲームに使うには躊躇するレベルです。が、私が作品の中で表現したいテーマとして、自然界そのものを表現したい心があります。自然界の現象と、機械言語による0or1表現は相反するもの。3次曲線はいずれも自然界に存在する形状に近い感覚がありますが、その分計算量は相当なものです。 しかし機械的でない、曲線の流れや柔らかさ、脈動感は、この3次曲線なしには表現できないだろうとも思ってます。これを実装したい。。。それが為に他の無駄を削る。削る。。。
とはいえ、3次曲線の実装のリスクは把握しておかねばなりません。。こいつはまともな計算方法だと最終的にフリーズしかねないくらい重いです(あくまでも当時の私の環境下で)
3次曲線上の座標を求める関数
/* 3次ベジェ曲線の数式(0 <= t <=1) t地点の座標を求める*/
fx(t) { return this.d3x*t*t*t + 3*this.d2x*t*t + 3*this.dx*t + this.x; } //tを代入してX座標取得
fy(t) { return this.d3y*t*t*t + 3*this.d2y*t*t + 3*this.dy*t + this.y; } //tを代入してY座標取得
例えば、3次曲線上の座標を求める計算。3乗計算ですね。これを当たり判定の度に*分割数だけ計算する。中々に大変そうです。それからaabb矩形を抜き出すのも4隅の座標を求める際に、極値となる2次方程式の解(最大で4回も)を求める必要があるので、尚更相当なものです。当初、毎フレーム極値を求める計算をしてて、曲線一個で処理時間がパンクしそうになりました。。。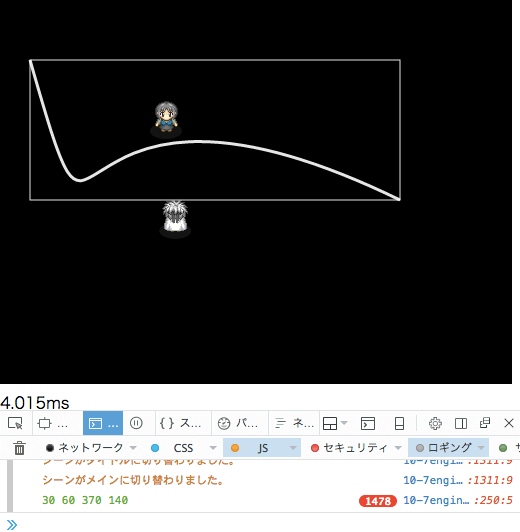
許容できるのが14~5msくらいで、一気に1/3が持ってかれてます。フリーな曲線3つでアウトだよ。。。そのため、一度3次曲線を設置したら、以降は動かさない。そのように自分ルール決めて、何とかキャッシュを活用しながら実用レベルにまで落とし込んだのでした。
実装までの過程は⇒3次ベジェ曲線と当たり判定式にメモしておきましたが、最後に書ききれてない「分割した座標を配列にキャッシュする」について、ここで取り上げたいと思います。
曲線の分割レベルから、何分の一で分割するかを数値化する
this.divNumber = 1 << divLevel; // 曲線判定の分割数は、2のn乗とする n=分割レベル。初期値は32分割となるよう調整
// = Math.pow(2, divLevel);
hitTestでは3次曲線を分割しながら当たり判定をとるのですが、分割数は、その分割レベルに応じて2乗計算で増やしていってます。
分割レベルをnとするなら、2のn乗を分割数で定義。分割レベルとシフト演算について
- レベル0なら分割数1
- レベル1なら分割数2
- レベル2なら分割数4
- レベル3なら分割数8
- レベル4なら分割数16
- レベル5なら分割数32
どこかで見た数字の並び...そう2進数です。 n乗計算の元が整数であれば、これは左シフト演算<<というのを使って計算を簡略化することができます。
例えば、1 << 5 という計算は32になります。 どういうことかというと、まず整数値の基準に1を与えてあげましょう。
1を2進数で表す
| 2進数の位 | 32 | 16 | 8 | 4 | 2 | 1 |
| 値が存在する? | 0 | 0 | 0 | 0 | 0 | 1 |
1<<5 を2進数で表す
| 2進数の位 | 32 | 16 | 8 | 4 | 2 | 1 |
| 値が存在する? | 1 | 0 | 0 | 0 | 0 | 0 |
まぁ同様に適当な値を2倍、4倍、8倍にするにも、このシフト演算の表記でいけます。
左シフト演算の活用例
2 << 1 = 2*2 = 4 2 << 2 = 2*4 = 8 2 << 3 = 2*8 = 16注意点として、元の数は整数に限定されること(計算時に小数点以下は切り捨てになります)。それから掛ける値を2の累乗分でしか活用できないことでしょう。用途は限られますが...シフト演算はその特性から、2分割を繰り返すような処理や配列と組み合わせるのに、非常に相性が良いものと思われます(4分木空間分割にもシフト演算が役立ってた気がする)
this.divNumber = 1 << divLevel; // 曲線判定の分割数は、2のn乗とする n=分割レベル。初期値は32分割となるよう調整
// = Math.pow(2, divLevel);
話を戻して、シフト演算で分割数を2の指定数乗で求めます。初期値は32となるようにしてます。
分割した曲線の座標を配列に格納してしまう
tArray(divNumber) { // 曲線上のtをdivNumberだけ分割した、それぞれの座標を配列でreturnする
const tArray = [];
for (let i=0; i <= divNumber; i++) {
const t = i * this.clipT;
tArray.push( {x:this.fx(t), y:this.fy(t)} );
}
return tArray;
}
そしてこの分割数を元に0<=t<=1で変化する3次曲線を分割して、初期値の場合は32個分の点の座標を配列に格納してしまおうという流れです。tを1/32ずつ変化させながら、配列にf(t)座標を追加していきます。...this.tArray[0] => {x:fx(0), y:fy(0)}
...this.tArray[1] => {x:fx(1/32), y:fy(1/32)}
...this.tArray[2] => {x:fx(2/32), y:fy(2/32)}
...
...
...this.tArray[32] => {x:fx(1), y:fy(1)}
配列のインデックス番号をdivNumber(分割数)で割ると、tの値となります。このようにすると、fx(t)とfy(t)の3次関数を計算せずに、即座に座標点を割り出せるので早いです。 ただしtの値を得る時は配列のインデックス番号からdivNumber(分割数)で割る必要がでてきます...そこはご愛嬌。よって1/divNumberもclipT要素として追加。
tではなく、配列のインデックス番号を基準に考える
後は配列のインデックス番号で曲線の範囲が与えられた時、極値が含まれてるかどうかをチェックする必要があります。この場合も極値となるtに分割数をかければ、インデックス番号との比較ができるようになります。
// 求めたtの極値から、配列のインデックス番号と比較できる値を求める *this.divNumber
this.X_LimIndex = this.xLimT.map( (t) => t *this.divNumber );
this.Y_LimIndex = this.yLimT.map( (t) => t *this.divNumber );
ここまで準備できれば、インデックス番号が与えられた範囲でのaabb4隅が求まるでしょう。
yMinMax(i0, i1) { /* iインデックス番号がi0〜i1における範囲の、yの最大最小を求める(初期値は0 <= t <=1 にthis.divNumberをかけた値*/
//const i0 = t0*this.divNumber, i1 = t1*this.divNumber; // tに曲線の分割数を掛ける、これが曲線を分割した座標の配列にアクセスできるインデックス値になる
const yCheck = [this.tArray[i0].y, this.tArray[i1].y]; // 両端のy座標を配列から取り出し、チェックリストに追加
for (let i=0; i < this.Y_LimIndex.length; i++) { // 極値となるtが範囲内か順番に確認
if( i1 <= this.Y_LimIndex[i] ) { return { min:Math.min(...yCheck), max:Math.max(...yCheck) }; } // 昇順なので、すでに大きい場合はこの時点で結果をreturnできる
if( i0 < this.Y_LimIndex[i] ) { yCheck.push(this.YnoKIWAMI[i]); } // もし極値となるtが範囲内なら、極値の座標もチェックリストに加える
}
return { min:Math.min(...yCheck), max:Math.max(...yCheck) }; // 範囲内のyの最小値と最大値を返す
}
xMinMax(i0, i1) { /* tがt0〜t1における範囲の、xの最大最小を求める(初期値は0 <= t <=1 にthis.divNumberをかけた値*/
//const i0 = t0*this.divNumber, i1 = t1*this.divNumber; // tに曲線の分割数を掛ける、これが曲線を分割した座標の配列にアクセスできるインデックス値になる
const xCheck = [this.tArray[i0].x, this.tArray[i1].x]; // 両端のy座標を配列から取り出し、チェックリストに追加
for (let i=0; i < this.X_LimIndex.length; i++) { // 極値となるtが範囲内か順番に確認
if( i1 <= this.X_LimIndex[i] ) { return { min:Math.min(...xCheck), max:Math.max(...xCheck) }; } // 昇順なので、すでに大きい場合はこの時点で結果をreturnできる
if( i0 < this.X_LimIndex[i] ) { xCheck.push(this.XnoKIWAMI[i]); } // もし極値となるtが範囲内なら、極値の座標もチェックリストに加える
}
return { min:Math.min(...xCheck), max:Math.max(...xCheck) }; // 範囲内のxの最小値と最大値を返す
}
で、曲線全体のaabb4隅(left,top,right,bottom)を求めるのに、最初にチェックをかけます。
const yMinMax = this.yMinMax(0, this.divNumber);
const xMinMax = this.xMinMax(0, this.divNumber);
分割数をインデックスの最大値にしてあげることで、曲線全体でのxの最小最大値、yの最小最大値が求まります。
this.top = yMinMax.min; //tが0〜1の間のyの最小値が上端
this.bottom = yMinMax.max; //tが0〜1の間のyの最大値が下端
this.left = xMinMax.min; //tが0〜1の間のxの最小値が左端
this.right = xMinMax.max; //tが0〜1の間のxの最大値が右端
この流れで4隅の値が求まります。計算量が半端ないので、もうキャッシュに固定です。3次曲線と矩形との当たり判定式を書き換え
hitRectBezierCurve(Rect, bezierCurve) { //矩形と3次ベジェ曲線の当たり判定導入部
const timeIndex = []; // 交点となる場合のt*分割数の値をリストに格納する
if( this.hitRectPoint(Rect, bezierCurve.x, bezierCurve.y) ) {timeIndex.push(0); return timeIndex;} //始点判定、trueならt=0で当たり。
if( this.hitRectPoint(Rect, bezierCurve.x3, bezierCurve.y3) ) {timeIndex.push(bezierCurve.divNumber); return timeIndex;} //終点判定、trueならt=1で当たり。
this.hitRectBezierCurve1_2(Rect, bezierCurve, 0, bezierCurve.divNumber, timeIndex); //それ以外なら始点t=0から終点t=1までの曲線を2分割してそれぞれのaabb判定から繰り返し
if( timeIndex.length > 0 ) { return timeIndex;} // 交点となるt*分割数の値が存在するなら、そのリストを返す(true判定)
return false;
}
hitRectBezierCurve1_2(Rect, bezierCurve, i0, i1, timeIndex) { //矩形と、t0〜t1までを2分割した3次曲線との当たり判定、再帰関数
const i0_5 = i0 + (i1 - i0) *0.5; // t範囲の半分の位置を定義
if( i1 - i0 >= 2 ) { // 分割数が余裕あるなら、tの範囲を2分割してaabb判定を繰り返す
if( this.hitRectPoint(Rect, bezierCurve.tArray[i0_5].x, bezierCurve.tArray[i0_5].y) ) { timeIndex.push(i0_5); } //中間地点の座標と接触なら当たり!
const bezierRect1 = bezierCurve.aabbRect2(i0, i0_5);
if( this.hitRectRect(Rect, bezierRect1) ) { this.hitRectBezierCurve1_2(Rect, bezierCurve, i0, i0_5, timeIndex); } //分割した矩形と接触ならさらに2分割して調査
const bezierRect2 = bezierCurve.aabbRect2(i0_5, i1);
if( this.hitRectRect(Rect, bezierRect2) ) { this.hitRectBezierCurve1_2(Rect, bezierCurve, i0_5, i1, timeIndex); } //同上
}
else { // 分割数の限界まで達したら、最後は直線で判定
const bezierLine = new Line(bezierCurve.tArray[i0].x, bezierCurve.tArray[i0].y, bezierCurve.tArray[i1].x, bezierCurve.tArray[i1].y);
if(this.hitRectLine(Rect, bezierLine)) {timeIndex.push(i0_5);}
}
}
3次曲線と接触した際のバウンス処理
otherCurveBounce(my, curve, info) { //曲線相手とのバウンス処理
const tSum = info.reduce((a, c) => a + c); // 交点となるt(或いはインデックス番号)の解の和(複数の場合)
const clipT = curve.hitArea.clipT || 1; // infoを分割数で割ると、tの値が出る。分割数がないなら1
const t = tSum * clipT / info.length; // tの解の平均値を得る、このtから法線ベクトルを求める
//const otherCx = curve.hitArea.fx(t), otherCy = curve.hitArea.fy(t); 曲線上のバウンドの起点となるXとYの座標を求める
const delta = new Vector2D (my.hitArea.cx - curve.hitArea.fx(t), my.hitArea.cy - curve.hitArea.fy(t)); //曲線上のバウンドの起点から自分の中心点までのベクトルで、お互いの位置関係を取得
const bounceVect = curve.hitArea.bounceVect(t).normalVect; // 法線の単位ベクトルを取得する(バウンド方向)
if(bounceVect.innerP(delta) < 0 && !curve.isFall) {bounceVect.dx*=-1; bounceVect.dy*=-1;} // もし法線が逆さ(内積が負)なら、ベクトルを逆向きにする。
let speed = my.speed; //法線ベクトルの大きさ。基本はこのアクターの速さ
speed = my.vector.length > speed ? my.vector.length : speed; //もし自分の移動ベクトルが(押し戻しなどの影響で)自分の速度より大きくなってるなら、移動ベクトルの大きさを反動の大きさとする。
my._velocityX += speed * bounceVect.dx *1.0625; //X軸の反動の大きさを反映 乗り越えを防ぐのに、反動の大きさ1/16増し。
my._velocityY += speed * bounceVect.dy *1.0625; //Y軸の反動の大きさを反映
}
曲線、長かったですね。成果はこちらです。矩形アクター100個、曲線2つ、人物2人。
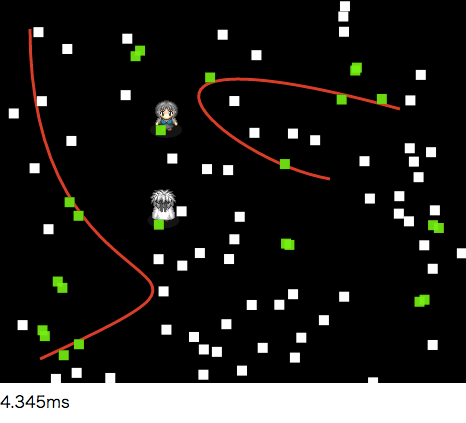
ちなみに3次曲線との判定式は、矩形としか反応させないようにしてるんで。 もし曲線の通行判定を無視できるアクターなら、円形クラスとかで使い分けできます。
円形アクター100個での処理速度。十分に実用レベルでしょう。
ここまでで、当たり判定まわりの実装は一段落です!おつかれさまでした。
休憩後、次はメッセージウィンドウ周りの実装に移りたいと思います。これまでと比べたら、ウィンドウ周りの難易度はやさしく感じると思います!
⇒ JavaScriptでゲーム作り「13:メッセージウィンドウを実装する」
古都さんのフレームワークを元にほぼ最初から作ってます。
たぶん順番に見ないとちんぷんかんぷん(' '*)...
すぺしゃるさんくす
https://sbfl.net/古都さん
JavaScriptで作る弾幕STGの基礎(フレームワーク)を使わせていただいてます。感謝!

ぴぽやさんもありがとう、キャラチップをお借りしています。