10-2:2次ベジェ曲線の当たり判定
ベジェ曲線の完成形デモはこんな感じです。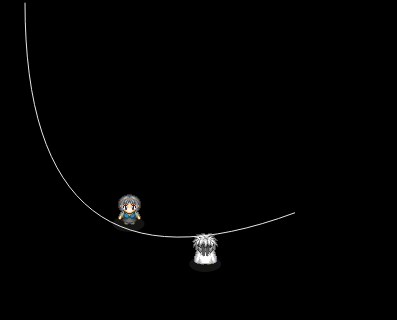
⇒ ベジェ曲線とキャラクター(矩形)のバウンス判定デモを見る
ベジェ曲線を実装する
(2019.3.14執筆)
これまで、矩形と円と直線(線分)の当たり判定を実装しました。ここに曲線が加わります。 マップの通行判定は線分のみでもいけるのですが、ベジェ曲線を使うと自然界に添うような地形を描ける感じです。 これが、背景描画の下書きに役立ったりするんじゃないかって思ったりしてます。ベジェ曲線(bezier-curve)の実装・当たり判定とバウンス処理。
しかし今回の実装は、技術的にかなり面倒くさいのに、別に無くてもゲーム進行に支障はない。 どちらかと言えばデザイン重視の行程になるので、読み飛ばし推奨かも。。。 余力ある人か、曲線の判定に挑戦してみたい方は、読んでみてください。
- ベジェ曲線とは何か
- ベジェ曲線をシーンに描画する
- ベジェ曲線とオブジェクト同士の当たり判定
- 交点とバウンス処理の計算を求める
今回の議題について、このような手順で進めようと思います。
ベジェ曲線とは何か
曲線の実装(最初は円の扇型でやろうとしていた)を調べていた時、ベジェ曲線というのを初めて知りました。 直線を、弓なりのように曲げた感じの線という印象。まっすぐの弓(直線)に力の加わる方向を1点。2点。と制御することで、直線だったものが自然なカーブを描くようになる。こちらの解説記事が図解入りで解りやすかったです。
⇒ 一から学ぶベジェ曲線
ベジェ曲線を描画する方法
解説読んでばかりでも、どーにもならん。実際に曲線を描いてみよう。どんな感じになるかな。。。⇒ canvasで様々な図形を描く(MDN)
こちらの記事から、canvasのcontextを使って描画する記述方法を抜き出してっと。
二次ベジェ曲線の描き方
quadraticCurveTo(cp1x, cp1y, x, y)
現在のペンの位置から x および y で指定した終端へ、cp1x および cp1y で指定した制御点を使用して二次ベジェ曲線を描きます。
(サンプルコード)
var ctx = canvas.getContext('2d');
// 二次ベジェ曲線の例
ctx.beginPath();
ctx.moveTo(75,25);
ctx.quadraticCurveTo(25,25,25,62.5);
ctx.fill();
2次ベジェ曲線。ベジェ曲線の基本形。
2次ペジェ曲線のラインは放物線の一部になるそうだ。
三次ベジェ曲線の描き方
bezierCurveTo(cp1x, cp1y, cp2x, cp2y, x, y)
現在のペンの位置から x および y で指定した終端へ、(cp1x, cp1y) および (cp2x, cp2y) で指定した制御点を使用して三次ベジェ曲線を描きます。(出典元:canvasで様々な図形を描く(MDN))
(サンプルコード)
var ctx = canvas.getContext('2d');
// 三次ベジェ曲線の例
ctx.beginPath();
ctx.moveTo(75,40);
ctx.bezierCurveTo(75,37,70,25,50,25);
ctx.fill();
実際に使用したいのはこの3次ペジェ曲線の方。曲線ラインが綺麗に見えます。
抜き出した例としてはこんなものでしょうか。
では製作中ゲームのシーンに、それぞれのベジェ曲線を登場させてみます。
ベジェ曲線クラス定義
これまでの資料を元に、2次ベジェ曲線、3次ベジェ曲線のクラスを定義、描画方法まで記述します。2次ベジェ曲線(quadraticCurve)クラスの定義と描画
class quadraticCurveActor extends Actor { //2次ベジェ曲線
constructor(x, y, cp1x, cp1y, x2, y2, tag, isFall=false) {
const hitArea = new Line(x, y, x2, y2, tag); //ここは後から変更します
super(x, y, hitArea, ['object']);
this.x2 = x2; //終着点のx座標
this.y2 = y2; //終着点のy座標
this.cp1x = cp1x; //制御点1のx座標
this.cp1y = cp1y; //制御点1のy座標
this.isFall = isFall; //一方通行にするかどうか
this._color = 'rgba(255, 255, 255, 0.9)'; //線画の色指定
this.addEventListener('hit', (e) => this._color = 'rgba(255, 0, 0, 0.9)' ); //当たり判定の時に赤くする
}
get x() { return this._x; } set x(value) { this._x = value; this.hitArea.x = value; }//x座標に値を代入する関数をActorから上書き
get y() { return this._y; } set y(value) { this._y = value; this.hitArea.y = value; }//y座標に値を代入する関数をActorから上書き
update(gameInfo, input) {
this._color = 'rgba(255, 255, 255, 0.9)';
}
render(target, scroller) {
const context = target.getContext('2d');
context.strokeStyle = this._color;
context.lineWidth = 3;
context.beginPath(); //描画位置の初期化
context.moveTo(this.x + scroller.x, this.y + scroller.y); //曲線のスタート位置を指定(画面スクロール分、それぞれの座標位置をずらしてます)
context.quadraticCurveTo(this.cp1x + scroller.x, this.cp1y + scroller.y,
this.x2 + scroller.x, this.y2 + scroller.y); //制御点1、終着点をそれぞれ指定して曲線の軌道を描く
context.stroke(); //軌道に沿って線を引く
}
}
3次ベジェ曲線(bezierCurve)クラスの定義と描画
class bezierCurveActor extends Actor { //3次ベジェ曲線
constructor(x, y, cp1x, cp1y, cp2x, cp2y, x2, y2, tag, isFall=false) {
const hitArea = new Line(x, y, x2, y2, tag); //ここは後から変更します
super(x, y, hitArea, ['object']);
this.x2 = x2; //終着点のx座標
this.y2 = y2; //終着点のy座標
this.cp1x = cp1x; //制御点1のx座標
this.cp1y = cp1y; //制御点1のy座標
this.cp2x = cp2x; //制御点2のx座標
this.cp2y = cp2y; //制御点2のy座標
this.isFall = isFall; //一方通行にするかどうか
this._color = 'rgba(255, 255, 255, 0.9)'; //線画の色指定
this.addEventListener('hit', (e) => this._color = 'rgba(255, 0, 0, 0.9)' ); //当たり判定の時に赤くする
}
get x() { return this._x; } set x(value) { this._x = value; this.hitArea.x = value; }//x座標に値を代入する関数をActorから上書き
get y() { return this._y; } set y(value) { this._y = value; this.hitArea.y = value; }//y座標に値を代入する関数をActorから上書き
update(gameInfo, input) {
this._color = 'rgba(255, 255, 255, 0.9)';
}
render(target, scroller) {
const context = target.getContext('2d');
context.strokeStyle = this._color;
context.lineWidth = 3;
context.beginPath(); //描画位置の初期化
context.moveTo(this.x + scroller.x, this.y + scroller.y); //曲線のスタート位置を指定
context.bezierCurveTo(this.cp1x + scroller.x, this.cp1y + scroller.y,
this.cp2x + scroller.x, this.cp2y + scroller.y,
this.x2 + scroller.x, this.y2 + scroller.y); //制御点1、制御点2、終着点をそれぞれ指定して曲線の軌道を描く
context.stroke(); //軌道に沿って線を引く
}
}
こんな感じでしょうか。当コラムの6章(ラインを引く)のLineActorを元に、曲線クラス「bezierCurveActor」を定義してみました。 あとはシーンに、bezierCurveクラスのインスタンスを追加するだけです。
シーンにbezierCurveを追加
class MainScene extends Scene {
constructor(renderingTarget) {
super('メイン', 1800, 1600, 'black', renderingTarget);
const npc = new NPC(150, 100);
this.add(npc);
this.add(global.player);
const Curve1 = new quadraticCurveActor (10, 30, 30, 340, 300, 240, 'wall');
this.add(Curve1);
const Curve2 = new bezierCurveActor (0, 0, 100, 60, 400, 60, 500, 360, 'wall');
this.add(Curve2);
}
}
数字は適当。さて、どうでしょう?

⇒ ベジェ曲線のデモを見る
ふむ、当たり判定は始点から終点までのLineそのままだが、いい感じに描けてます。第一段階クリア。
では次に、ベジェ曲線の当たり判定(交差判定)について考えることにします。まず2次ベジェ曲線で考える方が良かろう。
2次ベジェ曲線の交差判定
当たり判定の計算は、曲線とLineとの交差判定がベースになってくるようです。曲線上のX座標とY座標を求める数式を、直線の式(XとYの関係性)に代入して、式が成立てば交差点があるという仕組み。
ベジェ曲線の数式について、ちょっと参考になりそうな資料をば。。。
⇒ https://ja.javascript.info/bezier-curve
⇒ 二次ベジェ曲線と線分の当たり判定
これらを読んで考察、ベジェ曲線(と直線)の交差判定の手順を考えてみよう。
そして3時間かけて練ったアイデアがこちら。
2次ベジェ曲線の当たり判定の手順
1:まず曲線上のxの最小値と最大値、yの最小値と最大値をそれぞれ求める曲線の左端 = xの最小値 曲線の上端 = yの最小値 曲線の右端 = xの最大値 曲線の下端 = yの最大値
2:求めた四隅でAABBの矩形を作り、最初の当たり判定。この時点で外れなら当たってない(falseをreturnできる、判定高速化のため)。
3:もしAABB範囲内なら、曲線の数式を直線の式に代入して、交点の在り処を求める。。。
4:求めた交点が曲線上に存在し、かつ線分上にも存在するなら当たり!
5:それ以外なら外れ。。
こんな感じかな???
ひとまず、Colliderクラス(当たり判定に使うクラス)の拡張で2次ベジェ曲線を定義することにします。
2次ベジェ曲線 extends Colliderクラスの定義
class QuadraticCurve extends Collider { //当たり判定を2次ベジェ曲線で扱うクラス
constructor(x, y, cp1x, cp1y, x2, y2, tag) {
super('quadraticCurve', x, y, tag);
this.x2 = x2; //終着点のx座標
this.y2 = y2; //終着点のy座標
this.cp1x = cp1x; //制御点1のx座標
this.cp1y = cp1y; //制御点1のy座標
}
/* 2次ベジェ曲線の方程式(0 <= t <=1) */
fx(t) { return (this.x2 - 2*this.cp1x + this.x)*t*t + 2*t*(this.cp1x - this.x) + this.x; }
fy(t) { return (this.y2 - 2*this.cp1y + this.y)*t*t + 2*t*(this.cp1y - this.y) + this.y; }
get top() { return } // 曲線の上端 = yの最小値
get bottom() { return } // 曲線の下端 = yの最大値
get left() { return } // 曲線の左端 = xの最小値
get right() { return } // 曲線の右端 = xの最大値
}
そうだ、前もっての予備知識。
2次ペジェ曲線の計算式は、上のCollider定義に当て嵌めるとこんな感じらしい。。。
2次ペジェ曲線の計算式
/* 2次ベジェ曲線の方程式(0 <= t <=1) */ 曲線上のX座標 = fx(t) = (x2 - 2*cp1x + x)*(t**2) + 2*t*(cp1x - x) + x; 曲線上のY座標 = fy(t) = (y2 - 2*cp1y + y)*(t**2) + 2*t*(cp1y - y) + y;
プログラム言語、読みづらくてしゃーない。
もう、こういうものだと腹をくくるしか...(o _ o。)
あ、tっていうのは「0 <= t <= 1」の範囲で動く定数みたいなもので、この「t」に0から1までを代入して得られた各x,yの値が、曲線上の( x座標、y座標 )の連続した点となって連なっていく感覚。あああ。文字でも説明しづらい。取説はリンク先の図解でどうぞ。
⇒ https://ja.javascript.info/bezier-curve
ちなみにt=0の時は、始点の(x, y)座標が求まるし、
t=1の時は、終点の(x2, y2)となるのが数式から確認できます。
では、当たり判定の手順1にそって、
曲線内におけるXとYの最小・最大値をそれぞれ求めてみます。
このXが極値(最小値or最大値)になるtの定数と
このYが極値(最小値or最大値)になるtの定数とを
それぞれ求める式があります。
Xが極値になる定数「t」を求める式
0 = 2*t*(x2 - 2*cp1x + x) + 2*(cp1x - x) これをtについて解くと t = - (cp1x - x) / (x2 - 2*cp1x + x)Xの曲線式を微分した数式「2*t*(x2 - 2*cp1x + x) + 2*(cp1x - x) = 0」(一番凸な地点を調べる方法)から、どの位置で「Xの極値」に接するか。を計算するような感じでしょうか。
Yが極値になる定数「t」を求める式
0 = 2*t*(y2 - 2*cp1y + y) + 2*(cp1y - y) これをtについて解くと t = - (cp1y - y) / (y2 - 2*cp1y + y)こちらYの曲線式を微分した数式「2*t*(y2 - 2*cp1y + y) + 2*(cp1y - y) = 0」(一番凸な地点を調べる方法)から、どの位置で「Yの極値」に接するか。を計算するような感じでしょうか。
曲線の上端...Yの最小値を求める
get top() { // 曲線の上端 = Yの最小値
if(Math.min(y, cp1y, y2) !== cp1y) { //もし最小値が制御点cp1yでないなら
return Math.min(y, y2); //始点か終点のうち、どちらか小さい方が最小値。
}
else { //もし最小値が制御点cp1yとなるなら、t = - (cp1y - y) / (y2 - 2*cp1y + y);を曲線の式に代入してYの極値を求める
const t = - (cp1y - y) / (y2 - 2*cp1y + y);
const y3 = (y2 - 2*cp1y + y)*t*t + 2*t*(cp1y - y) + y;
return y3; //極値が最小値。
}
}
試しに曲線の上端(Y座標の最小値)を求める...get top() {}の関数を設定してみました。こんなもんですかね。
曲線の下端...Yの最大値を求める
get bottom() { // 曲線の下端 = Yの最大値
if(Math.max(y, cp1y, y2) !== cp1y) { //もし最大値が制御点cp1yでないなら
return Math.max(y, y2); //始点か終点のうち、どちらか大きい方が最大値。
}
else { //もし最大値が制御点cp1xとなるなら、t = - (cp1y - y) / (y2 - 2*cp1y + y);を曲線の式に代入してYの極値を求める
const t = - (cp1y - y) / (y2 - 2*cp1y + y);
const y3 = (y2 - 2*cp1y + y)*t*t + 2*t*(cp1y - y) + y;
return y3; //極値が最大値。
}
}
同様にYの最大値(曲線の下限)もやってみました。うむ、Math.minをMath.maxに置き換えた流れ作業である。
x軸(左右端)の方も同様にやってみよう...
曲線の左端...Xの最小値を求める
get left() { // 曲線の左端 = Xの最小値
if(Math.min(x, cp1x, x2) !== cp1x) { //もし最小値が制御点cp1xでないなら
return Math.min(x, x2); //始点か終点のうち、どちらか小さい方が最小値。
}
else { //もし最小値が制御点cp1xとなるなら、t = - (cp1x - x) / (x2 - 2*cp1x + x);を曲線の式に代入してXの極値を求める
const t = - (cp1x - x) / (x2 - 2*cp1x + x);
const x3 = (x2 - 2*cp1x + x)*t*t + 2*t*(cp1x - x) + x;
return x3; //極値が最小値。
}
}
曲線の右端...Xの最大値を求める
get right() { // 曲線の右端 = Xの最大値
if(Math.max(x, cp1x, x2) !== cp1x) { //もし最大値が制御点cp1xでないなら
return Math.max(x, x2); //始点か終点のうち、どちらか大きい方が最大値。
}
else { //もし最大値が制御点cp1xとなるなら、t = - (cp1x - x) / (x2 - 2*cp1x + x);を曲線の式に代入してXの極値を求める
const t = - (cp1x - x) / (x2 - 2*cp1x + x);
const x3 = (x2 - 2*cp1x + x)*t*t + 2*t*(cp1x - x) + x;
return x3; //極値が最大値。
}
}
はい、これで2次ペジェ曲線の4隅の点が求まりました。 この4隅の点から、aabb矩形を求めることが出来ます。
求めた4隅の点から、曲線と接するaabb矩形を抜き出す。
get aabbRect() { // 曲線と接するaabb矩形
return new Rectangle( this.left, this.top, this.right - this.left, this.bottom - this.top);
}
この矩形が、衝突するかどうかの最初の判定(falseか否か?)で活用されます。
ここまでの関数を2次ペジェ曲線のColliderクラスにまとめると、以下のようになります。
あああ、ありがちなミスだけど、xなどの要素を指定する際にthis.xとするのを忘れていた。補完しております。
ここまでの2次ペジェ曲線Colliderクラスのまとめ
class QuadraticCurve extends Collider { //当たり判定を2次ベジェ曲線で扱うクラス
constructor(x, y, cp1x, cp1y, x2, y2, tag) {
super('quadraticCurve', x, y, tag);
this.x2 = x2; //終着点のx座標
this.y2 = y2; //終着点のy座標
this.cp1x = cp1x; //制御点1のx座標
this.cp1y = cp1y; //制御点1のy座標
}
/* 2次ベジェ曲線の方程式(0 <= t <=1) */
fx(t) { return (this.x2 - 2*this.cp1x + this.x)*t*t + 2*t*(this.cp1x - this.x) + this.x; }
fy(t) { return (this.y2 - 2*this.cp1y + this.y)*t*t + 2*t*(this.cp1y - this.y) + this.y; }
get top() { // 曲線の上端 = Yの最小値
if(Math.min(this.y, this.cp1y, this.y2) !== this.cp1y) { //もし最小値が制御点cp1yでないなら
return Math.min(this.y, this.y2); //始点か終点のうち、どちらか小さい方が最小値。
}
else { //もし最小値が制御点cp1yとなるなら、t = - (cp1y - y) / (y2 - 2cp1y + y);を曲線の式に代入してYの極値を求める
const t = - (this.cp1y - this.y) / (this.y2 - 2*this.cp1y + this.y);
return this.fy(t); //極値が最小値。
}
}
get bottom() { // 曲線の下端 = Yの最大値
if(Math.max(this.y, this.cp1y, this.y2) !== this.cp1y) { //もし最大値が制御点cp1yでないなら
return Math.max(this.y, this.y2); //始点か終点のうち、どちらか大きい方が最大値。
}
else { //もし最大値が制御点cp1xとなるなら、t = - (cp1y - y) / (y2 - 2cp1y + y);を曲線の式に代入してYの極値を求める
const t = - (this.cp1y - this.y) / (this.y2 - 2*this.cp1y + this.y);
return this.fy(t); //極値が最大値。
}
}
get left() { // 曲線の左端 = Xの最小値
if(Math.min(this.x, this.cp1x, this.x2) !== this.cp1x) { //もし最小値が制御点cp1xでないなら
return Math.min(this.x, this.x2); //始点か終点のうち、どちらか小さい方が最小値。
}
else { //もし最小値が制御点cp1xとなるなら、t = - (cp1x - x) / (x2 - 2cp1x + x);を曲線の式に代入してXの極値を求める
const t = - (this.cp1x - this.x) / (this.x2 - 2*this.cp1x + this.x);
return this.fx(t); //極値が最小値。
}
}
get right() { // 曲線の右端 = Xの最大値
if(Math.max(this.x, this.cp1x, this.x2) !== this.cp1x) { //もし最大値が制御点cp1xでないなら
return Math.max(this.x, this.x2); //始点か終点のうち、どちらか大きい方が最大値。
}
else { //もし最大値が制御点cp1xとなるなら、t = - (cp1x - x) / (x2 - 2cp1x + x);を曲線の式に代入してXの極値を求める
const t = - (this.cp1x - this.x) / (this.x2 - 2*this.cp1x + this.x);
return this.fx(t); //極値が最大値。
}
}
get aabbRect() { // 曲線と接するaabb矩形
return new Rectangle( this.left, this.top, this.right - this.left, this.bottom - this.top);
}
}
ここで、ちょっとaabb矩形を可視化してみますか。
別の、2次曲線を描画するクラスの方で、aabb矩形も描き出してみます。
描画する2次ベジェ曲線のアクタークラスを以下のように書き換えてっと。
class quadraticCurveActor extends Actor { //2次ベジェ曲線
constructor(x, y, cp1x, cp1y, x2, y2, tag, isFall=false) {
const hitArea = new QuadraticCurve(x, y, cp1x, cp1y, x2, y2);
super(x, y, hitArea, ['object']);
this.x2 = x2; //終着点のx座標
this.y2 = y2; //終着点のy座標
this.cp1x = cp1x; //制御点1のx座標
this.cp1y = cp1y; //制御点1のy座標
this.isFall = isFall; //一方通行にするかどうか
this._color = 'rgba(255, 255, 255, 0.9)'; //線画の色指定
this.addEventListener('hit', (e) => this._color = 'rgba(255, 0, 0, 0.9)' ); //当たり判定の時に赤くする
}
get x() { return this._x; } set x(value) { this._x = value; this.hitArea.x = value; }//x座標に値を代入する関数をActorから上書き
get y() { return this._y; } set y(value) { this._y = value; this.hitArea.y = value; }//y座標に値を代入する関数をActorから上書き
update(gameInfo, input) {
this._color = 'rgba(255, 255, 255, 0.9)';
}
render(target, scroller) {
const context = target.getContext('2d');
context.strokeStyle = this._color;
context.lineWidth = 3;
context.beginPath(); //描画位置の初期化
context.moveTo(this.x + scroller.x, this.y + scroller.y); //曲線のスタート位置を指定(画面スクロール分、それぞれの座標位置をずらしてます)
context.quadraticCurveTo(this.cp1x + scroller.x, this.cp1y + scroller.y,
this.x2 + scroller.x, this.y2 + scroller.y); //制御点1、終着点をそれぞれ指定して曲線の軌道を描く
context.stroke(); //軌道に沿って線を引く
context.lineWidth = 1;
context.beginPath(); //ここからaabb矩形も可視化してみる。
context.strokeRect(this.hitArea.left, this.hitArea.top, this.hitArea.aabbRect.width, this.hitArea.aabbRect.height);
}
}

⇒ 2次ベジェ曲線に接するaabb矩形のデモを見る
よしよし、うまく曲線に接するaabb矩形が求められたようですね。
この矩形でまず当たり判定して、falseなら当たってない判定を返せる(判定を高速化できる)という感じです。
やっと2段階目ができたというところか...さ、次は、当たり判定の本番となる。
2次ベジェ曲線と、直線の交点を求める
当たり判定のメイン。曲線上のX座標とY座標を、直線の式に代入して交点を求める方法をとります。(参考)
⇒ 二次ベジェ曲線と線分の当たり判定
⇒ 二次方程式の解の公式
⇒ 二次ベジェ曲線と直線の交点
上のURLの解説を読むと、下のURLの記述が何となく分かる。
こちらもJavaScriptを用いて、数式でのプログラミングを実践してみました。こちら完成形です。
2次ベジェ曲線と直線の交点を求める式
deLineQCurve(line, qCurve) { //線分と2次ベジェ曲線の衝突判定式
if( !this.deRectLine(qCurve.aabbRect, line) ) {return false;} //2次曲線のaabb矩形と直線を判定して、falseならfalseを返して終了
/*
// 直線の式 dy*(X - x) = dx*(Y - y);
*/
/*2次ベジェ曲線の方程式(0 <= t <=1)
//X座標 = (x2 - 2*cp1x + x)*t*t + 2*(cp1x - x)*t + x;
//Y座標 = (y2 - 2*cp1y + y)*t*t + 2*(cp1y - y)*t + y;
*/
/*2次ベジェ曲線の定数(0 <= t <= 1) の間で変化するtを用いた数式*/
// X = (qCurve.x2 - 2*qCurve.cp1x + qCurve.x)*t*t + 2*(qCurve.cp1x - qCurve.x)*t + qCurve.x; //曲線上のX座標の値を定義
// Y = (qCurve.y2 - 2*qCurve.cp1y + qCurve.y)*t*t + 2*(qCurve.cp1y - qCurve.y)*t + qCurve.y; //曲線上のY座標の値を定義
//見づらいので、変数を定義してまとめる。
const QX2 = qCurve.x2 - 2*qCurve.cp1x + qCurve.x;
const QX1 = 2*(qCurve.cp1x - qCurve.x);
const QX0 = qCurve.x;
const QY2 = qCurve.y2 - 2*qCurve.cp1y + qCurve.y;
const QY1 = 2*(qCurve.cp1y - qCurve.y);
const QY0 = qCurve.y;
// X = QX2*t*t + QX1*t + QX0; //曲線上のX座標の値を定義
// Y = QY2*t*t + QY1*t + QY0; //曲線上のY座標の値を定義
//line.dy*X - line.dy*line.x = line.dx*Y - line.dx*line.y; //直線の式に当て嵌める。
//line.dy*X - line.dx*Y + line.dx*line.y - line.dy*line.x = 0; //ここに曲線の式...XとYの2次方程式(t)の値を代入し、tについて解く。
// tの2次方程式ができる。
/*
line.dy* (QX2*t*t + QX1*t + QX0)
- line.dx* (QY2*t*t + QY1*t + QY0)
+ line.dx*line.y - line.dy*line.x
= 0;
*/
// tについて解く。
/*
(line.dy*QX2 - line.dx*QY2)*t*t
+ (line.dy*QX1 - line.dx*QY1)*t
+ line.dy*QX0 - line.dx*QY0 + line.dx*line.y - line.dy*line.x
= 0;
*/
//解の公式を使うために、a*t*t + b*t + c = 0;の形に整理し、定数a,b,cの値を定義する。
const a = line.dy* QX2 - line.dx* QY2;
const b = line.dy* QX1 - line.dx* QY1;
const c = line.dy* QX0 - line.dx* QY0 + line.dx*line.y - line.dy*line.x;
const timeCurve = []; //tの解を格納する場所
//解の公式 t = (-b ± Math.sqrt(b*b - 4*a*c))/(2*a)
//解の公式を用いて2次方程式の定数tの値(2つある)を得る判定
const delta = b*b - 4*a*c; //Math.sqrt(b*b - 4*a*c))の中身を判定
if (delta < 0) {return false;} //delta が負に値になるとき、解はない。交点が存在しない
else if (delta === 0) { //delta=0 のとき、tの解は1つ。timeCurveリストにtの解を一つ追加する
timeCurve.push( -b/(2*a) ); //tの解 = -b/(2*a)
}
else if (delta > 0) { //delta>0 のとき、tの解は2つ。timeCurveリストにtの解を二つ追加する
timeCurve.push( (-b + Math.sqrt(delta))/(2*a) ); //tの解1つめ = -b + Math.sqrt(delta))/(2*a)
timeCurve.push( (-b - Math.sqrt(delta))/(2*a) ); //tの解2つめ = -b - Math.sqrt(delta))/(2*a)
}
for(let t of timeCurve) { //求めたtの解(timeCurveリストに格納)それぞれについて判定
if(0 <= t && t <= 1){ /*tの解が0 <= t <=1 のとき、直線Lineとの交点を持つ。その交点座標が線分上に存在するなら当たり!*/
const x3 = QX2*t*t + QX1*t + QX0; //交点のX座標を求める
const y3 = QY2*t*t + QY1*t + QY0; //交点のY座標を求める
if (line.x === line.x2 ) {//X座標が一定ならY座標判定へ
if ( line.y <= y3 && y3 <= line.y2 || line.y2 <= y3 && y3 <= line.y ) { return true; } //Y座標が線分上にあるなら当たり!
}
else if ( line.x <= x3 && x3 <= line.x2 || line.x2 <= x3 && x3 <= line.x ) { return true; } //X座標が線分上にあるなら当たり!
}
}
return false;
}
曲線と直線の数式を用いての当たり判定。試してみました。
解説はソース内にコメントで残してますが、追って説明を試みます。
まず2次曲線の式です、
X座標とY座標を、変数t(0〜1の間で変化するtimeCurveの値)という不定値を用いた2次方程式で表現します。
2次ベジェ曲線の方程式(0 <= t <=1)
//X座標 = (x2 - 2*cp1x + x)*t*t + 2*(cp1x - x)*t + x;
//Y座標 = (y2 - 2*cp1y + y)*t*t + 2*(cp1y - y)*t + y;
xとかcp1xとかx2とかは、2次曲線を描くときに定義した始点のx座標、制御点(1)のx座標、終点(2)のx座標で、ゲーム中では既に決まった値を持ちます。 0〜1に変化するtの値によって、曲線上のX座標がどこになるか?を。この式は表します。
そしてY座標についても同様に求めてます。
これらは共通する変数tの値を用いて、2次曲線上のXとY座標の関係性を示すものです。
直線(線分を延長した直線)の式
// 直線の式 dy*(X - x) = dx*(Y - y);
dy...というのは、Lineの項で定義した通り、線分の終点2のy座標から始点のy座標を引いた値。 dx...も同様、こちらは線分の終点2のx座標から、始点のx座標を引いた値です。
これも等価式 = の、直線上のXとY座標の関係性を示すものです。
2次曲線と直線の式で、共通するXとYの値を持つとき、交点が存在する
直線と曲線が交わるとき、X,Yはそれぞれ共通する値を持ちます。 この現象を再現するために、直線の式にあるXとYに、曲線のXとYの値をそのまま代入して、直線と2次曲線が交差するタイミングtの値を求めます。これはtの2次方程式になります。なお、2次方程式の解の公式を活用するため、〜*t*t + 〜*t + 〜 = 0...の式に整理する必要があります。
整理して、2次方程式tの解を求めます。
参考 ⇒ 二次方程式の解の公式
式が無駄に長いので、どうぞ読み飛ばしてください
式は、その意味(何をやってるか?)がわかれば、文字の羅列を覚える必要などありません。。時間の無駄です。
// 直線の式 の 両辺を、- dx*(Y - y) する。
//dy*(X - x) - dx*(Y - y) = 0;
//展開して整理する
//dy*X - dx*Y - dy*x + dx*y = 0
//この直線の式にあるXとYに、曲線の式を代入する
/*2次ベジェ曲線の方程式(0 <= t <=1)*/
//X座標 = (x2 - 2*cp1x + x)*t*t + 2*(cp1x - x)*t + x;
//Y座標 = (y2 - 2*cp1y + y)*t*t + 2*(cp1y - y)*t + y;
// dy*((x2 - 2*cp1x + x)*t*t + 2*(cp1x - x)*t + x) - dx*((y2 - 2*cp1y + y)*t*t + 2*(cp1y - y)*t + y) - dy*x + dx*y = 0
//非常に長い。アホか...と思える数式。
//この数式を短略化するのに、曲線の式の定数となる部分を文字列に置き換えると見やすくなる。
//X座標 = (x2 - 2*cp1x + x)*t*t + 2*(cp1x - x)*t + x;について
const QX2 = (x2 - 2*cp1x + x);
const QX1 = 2*(cp1x - x);
const QX0 = x;
//Y座標 = (y2 - 2*cp1y + y)*t*t + 2*(cp1y - y)*t + y;についても
const QY2 = qCurve.y2 - 2*qCurve.cp1y + qCurve.y;
const QY1 = 2*(qCurve.cp1y - qCurve.y);
const QY0 = qCurve.y;
//X座標 = QX2*t*t + QX1*t + QX0; の形にできる、
//Y座標 = QY2*t*t + QY1*t + QY0; の形にできる。
//これらXとYの数式を、直線dy*X - dx*Y - dy*x + dx*y = 0にあてはめてみると。。。
// dy* (QX2*t*t + QX1*t + QX0) - dx* (QY2*t*t + QY1*t + QY0) + dx*y - dy*x = 0;
//これを2次方程式tについて解く。
/*
(dy*QX2 - dx*QY2)*t*t
+ (dy*QX1 - dx*QY1)*t
+ dy*QX0 - dx*QY0 + dx*y - dy*x
= 0;
*/
//解の公式を使うために、a*t*t + b*t + c = 0;の形に整理し、定数a,b,cの値を定義する。
const a = dy* QX2 - dx* QY2;
const b = dy* QX1 - dx* QY1;
const c = dy* QX0 - dx* QY0 + dx* y - dy* x;
//解の公式 t = (-b ± Math.sqrt(b*b - 4*a*c))/(2*a)
//解の公式を用いて2次方程式の定数tの値(2つある)を得る
const timeCurveCheck = []; //2次方程式tの解を格納する場所
const delta = b*b - 4*a*c; //Math.sqrt(b*b - 4*a*c))の中身を判定...ここを先に判定すると早い。
if (delta < 0) {return false;} //delta が負に値になるとき、解はない。交点が存在しない
else if (delta === 0) { //delta=0 のとき、tの解は1つ。timeCurveリストにtの解を一つ追加する
timeCurveCheck.push( -b/(2*a) ); //t = -b/(2*a)
}
else if (delta > 0) { //delta>0 のとき、tの解は2つ。timeCurveリストにtの解を二つ追加する
timeCurveCheck.push( (-b + Math.sqrt(delta))/(2*a) ); //t = -b + Math.sqrt(delta))/(2*a)
timeCurveCheck.push( (-b - Math.sqrt(delta))/(2*a) ); //t = -b - Math.sqrt(delta))/(2*a)
}
ここまでの計算で、直線に交差する曲線上の点(X, Y)となるtの値が求まります。
そしてtの値が0〜1の間のとき、この曲線上に交点があると判定できる。
あとはtの値を曲線上の数式に代入し、その座標が線分上にあるかどうかを判定できれば、線分と曲線の交差判定ができるという形でした。
線分上に交点が存在するかどうか?
for(let t of timeCurveCheck) { //求めたtの解(timeCurveリストに格納)それぞれについて判定
if(0 <= t && t <= 1){ /*tの解が0 <= t <=1 のとき、直線Lineとの交点を持つ。その交点座標が線分上に存在するなら当たり!*/
const x3 = QX2*t*t + QX1*t + QX0; //交点のX座標を求める
const y3 = QY2*t*t + QY1*t + QY0; //交点のY座標を求める
if ( line.x <= x3 && x3 <= line.x2 || line.x2 <= x3 && x3 <= line.x ) {
if ( line.y <= y3 && y3 <= line.y2 || line.y2 <= y3 && y3 <= line.y ) {return true;}
}
}
}
長いですね。そして要素が多すぎてこんがらがる。
やれやれ... 面倒くさいが、やってることは、図面で表せば単純な感じです。
この数式計算を、プログラム上で実際に動かすとどうでしょう?
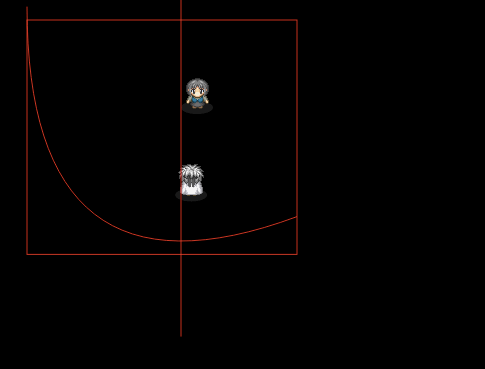
⇒ ベジェ曲線と直線の当たり判定デモを見る
えっと、問題が発生してます。
交差してるのに、当たってる判定が途切れる(色が点滅する)。なぜだ???
原因を探る...
数値を変え、直線に若干の傾きを与えた所、綺麗に判定されるのが確認できた。
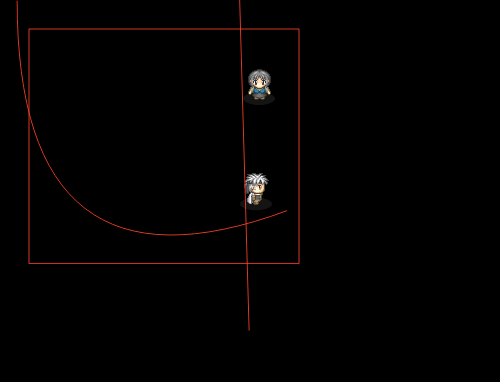
⇒ ベジェ曲線と直線2の当たり判定デモ
つまり、方程式の解は間違ってない。
しかし、直線の始点Xと終点Xが同じ時、y軸に平行な直線のとき、判定が抜ける...ことが伺えます。
なぜだろう...
JavaScriptの仕様で、思い当たる節がありました。
⇒ JavaScript 基礎と文法
このうちの浮動小数点の扱い(一番下に在る項目)についての解説です。
小数点以下の数値を計算するとき、計算結果に誤差が生まれるというもの。。。
曲線上の交点X = QX2*t*t + QX1*t + QX0; としたとき 直線の始点X0 <= 曲線上の交点X <= 直線の終点X2 或いは、直線の始点X0 >= 曲線上の交点X >= 直線の終点X2 のとき、線分と曲線の交点が存在する
という式で判定が(ほぼ)成り立つのですが、
直線がy軸に並行(始点X = 終点X2)のとき、その間から曲線上の交点X座標がはみ出てしまう現象が度々おこってしまうようで、それで当たり判定が抜け落ちてたのです。
対策として直線の始点Xと終点Xが同じ値の場合、Yの方で判定する方法をとります。これで現象が改善されると思う。
交点が線分上に存在するか?の判定式
for(let t of timeCurve) { //求めたtの解(timeCurveリストに格納)それぞれについて判定
if(0 <= t && t <= 1){ /*tの解が0 <= t <=1 のとき、直線Lineとの交点を持つ。その交点座標が線分上に存在するなら当たり!*/
const x3 = QX2*t*t + QX1*t + QX0; //交点のX座標を求める
const y3 = QY2*t*t + QY1*t + QY0; //交点のY座標を求める
if (line.x === line.x2 ) {//直線のX座標が一定ならY座標判定へ
if ( line.y <= y3 && y3 <= line.y2 || line.y2 <= y3 && y3 <= line.y ) { return true; } //Y座標が線分上にあるなら当たり!
}
else if ( line.x <= x3 && x3 <= line.x2 || line.x2 <= x3 && x3 <= line.x ) { return true; } //X座標が線分上にあるなら当たり!
}
}

⇒ ベジェ曲線と直線の当たり判定デモ3を見る
綺麗に判定できました。
これで2次ベジェ曲線と線分の当たり判定式が完了です。ふぅう。。。。。(ここまでで第3段階が終わった)
浮動小数点とか、何の罠でしょうね。。。こんなことが、プログラミングやってると、たまに在るようです。原因特定と修正に1〜2日かかった。
QuadraticCurveクラスを改良する
さて、直線との当たり判定式にて多用した曲線の値があります。
/*2次ベジェ曲線の定数(0 <= t <= 1) の間で変化するtを用いた数式*/
// X = (qCurve.x2 - 2*qCurve.cp1x + qCurve.x)*t*t + 2*(qCurve.cp1x - qCurve.x)*t + qCurve.x; //曲線上のX座標の値を定義
// Y = (qCurve.y2 - 2*qCurve.cp1y + qCurve.y)*t*t + 2*(qCurve.cp1y - qCurve.y)*t + qCurve.y; //曲線上のY座標の値を定義
//見づらいので、変数を定義してまとめる。
const QX2 = qCurve.x2 - 2*qCurve.cp1x + qCurve.x;
const QX1 = 2*(qCurve.cp1x - qCurve.x);
const QX0 = qCurve.x;
const QY2 = qCurve.y2 - 2*qCurve.cp1y + qCurve.y;
const QY1 = 2*(qCurve.cp1y - qCurve.y);
const QY0 = qCurve.y;
曲線上の点(X, Y)を求めるtの連立方程式。 このときに定義された値は、曲線上の様々な計算で使い回すことが想定されます。 QuadraticCurve本体の方に、予め値を定義しておいたほうが良さそうです。
2次ベジェ曲線クラスの改良後のソースコード
class QuadraticCurve extends Collider { //当たり判定を2次ベジェ曲線で扱うクラス
constructor(x, y, cp1x, cp1y, x2, y2, tag) {
super('quadraticCurve', x, y, tag);
this.x2 = x2; //終着点のx座標
this.y2 = y2; //終着点のy座標
this.cp1x = cp1x; //制御点1のx座標
this.cp1y = cp1y; //制御点1のy座標
/* 2次ベジェ曲線の方程式(0 <= t <=1) */
// 曲線上のX座標 = fx(t) = (this.x2 - 2*this.cp1x + this.x)*t*t + 2*(this.cp1x - this.x)*t + this.x;
this.QX2 = this.x2 - 2*this.cp1x + this.x; // 曲線上のX座標を求める方程式のt**2の係数
this.QX1 = 2*(this.cp1x - this.x); // 曲線上のX座標を求める方程式のt**1の係数
this.QX0 = this.x; // 曲線上のX座標を求める方程式のt**0の係数
// 曲線上のY座標 = fy(t) = (this.y2 - 2*this.cp1y + this.y)*t*t + 2*(this.cp1y - this.y)*t + this.y;
this.QY2 = this.y2 - 2*this.cp1y + this.y; // 曲線上のY座標を求める方程式のt**2の係数
this.QY1 = 2*(this.cp1y - this.y); // 曲線上のY座標を求める方程式のt**1の係数
this.QY0 = this.y; // 曲線上のY座標を求める方程式のt**0の係数
}
/* 2次ベジェ曲線の方程式(0 <= t <=1) t地点の座標を求める*/
fx(t) { return this.QX2*t*t + this.QX1*t + this.x; }
fy(t) { return this.QY2*t*t + this.QY1*t + this.y; }
/* 2次曲線の微分式(0 <= t <=1) の時の、曲線の傾きを求める */
f1x(t) { return 2*this.QX2*t + this.QX1; }
f1y(t) { return 2*this.QY2*t + this.QY1; }
bounceVect(t) { // tのときの曲線上の微分式から法線ベクトルを求める
const dx = this.f1x(t), dy = this.f1y(t);
return new Vector2D(-dy, dx); // 曲線のt地点における傾きに垂直なベクトル
}
get top() { // 曲線の上端 = Yの最小値
if(Math.min(this.y, this.cp1y, this.y2) !== this.cp1y) { //もし最小値が制御点cp1yでないなら
return Math.min(this.y, this.y2); //始点か終点のうち、どちらか小さい方が最小値。
}
else { //もし最小値が制御点cp1xとなるなら、t = - (cp1y - y) / (y2 - 2cp1y + y);を曲線の式に代入してYの極値を求める
if(this.y3 === undefined) {
const t = - (this.cp1y - this.y) / (this.y2 - 2*this.cp1y + this.y);
this.y3 = this.fy(t); //極値が最小値。
}
return this.y3;
}
}
get bottom() { // 曲線の下端 = Yの最大値
if(Math.max(this.y, this.cp1y, this.y2) !== this.cp1y) { //もし最大値が制御点cp1yでないなら
return Math.max(this.y, this.y2); //始点か終点のうち、どちらか大きい方が最大値。
}
else { //もし最大値が制御点cp1xとなるなら、t = - (cp1y - y) / (y2 - 2cp1y + y);を曲線の式に代入してYの極値を求める
if(this.y3 === undefined) {
const t = - (this.cp1y - this.y) / (this.y2 - 2*this.cp1y + this.y);
this.y3 = this.fy(t); //極値が最大値。
}
return this.y3;
}
}
get left() { // 曲線の左端 = Xの最小値
if(Math.min(this.x, this.cp1x, this.x2) !== this.cp1x) { //もし最小値が制御点cp1xでないなら
return Math.min(this.x, this.x2); //始点か終点のうち、どちらか小さい方が最小値。
}
else { //もし最小値が制御点cp1xとなるなら、t = - (cp1x - x) / (x2 - 2cp1x + x);を曲線の式に代入してXの極値を求める
if(this.x3 === undefined) {
const t = - (this.cp1x - this.x) / (this.x2 - 2*this.cp1x + this.x);
this.x3 = this.fx(t); //極値が最小値。
}
return this.x3;
}
}
get right() { // 曲線の右端 = Xの最大値
if(Math.max(this.x, this.cp1x, this.x2) !== this.cp1x) { //もし最大値が制御点cp1xでないなら
return Math.max(this.x, this.x2); //始点か終点のうち、どちらか大きい方が最大値。
}
else { //もし最大値が制御点cp1xとなるなら、t = - (cp1x - x) / (x2 - 2cp1x + x);を曲線の式に代入してXの極値を求める
if(this.x3 === undefined) {
const t = - (this.cp1x - this.x) / (this.x2 - 2*this.cp1x + this.x);
this.x3 = this.fx(t); //極値が最大値。
}
return this.x3;
}
}
get aabbRect() { // 曲線と接するaabb矩形
return new Rectangle( this.left, this.top, this.right - this.left, this.bottom - this.top);
}
}
すると、直線との判定式で定義していたQX2,QX1,QX0,QY2,QY1,QY0の6つもの変数を、大元の値.からそのまま呼び出せる形になるので、他のアクターとの判定にも値の使い回しが効きます。最終的なソースの簡略化にもなるし、計算処理の負担も少なそうです。
2次ベジェ曲線と矩形の当たり判定
では続いて矩形との当たり判定です。これは2次ベジェ曲線と線分との交差判定×4辺分で求められますが、 矩形の4辺には傾きが存在しないため、2次曲線との判定式の手順を少し簡略化することができます。
deRectQCurve(rect, qCurve) { //矩形と2次ベジェ曲線の衝突判定式
if( !this.deRectRect(rect, qCurve.aabbRect) ) {return false;} //矩形と2次曲線のaabb矩形を判定して、falseならfalseを返して終了
const timeCurve = []; //tの解で交点になる答えを格納(このオブジェクトの値を判定式で返す)
if( this.deRectPoint(rect, qCurve.x, qCurve.y) ) { timeCurve.push(0); return timeCurve; } //矩形と2次曲線の始点を判定、trueなら当たり。
if( this.deRectPoint(rect, qCurve.x2, qCurve.y2) ) { timeCurve.push(1); return timeCurve;} //矩形と2次曲線の終点を判定、trueなら当たり。
/*2次ベジェ曲線の定数(0 <= t <= 1) の間で変化するtを用いた数式*/
// X = QX2*t*t + QX1*t + QX0; //曲線上のX座標の値を定義
// Y = QY2*t*t + QY1*t + QY0; //曲線上のY座標の値を定義
/*
// 矩形の線分式1 X = rect.left; (Y >= rect.top, Y <= rect.bottom)
// 矩形の線分式2 X = rect.right; (Y >= rect.top, Y <= rect.bottom)
// 矩形の線分式3 Y = rect.top; (X >= rect.left, X <= rect.right)
// 矩形の線分式4 Y = rect.bottom; (X >= rect.left, X <= rect.right)
*/
// それぞれの矩形の式に、XやYを当てはめる。tの解について4回の判定をする
// tの2次方程式ができる。
/*
// 矩形の線分式1との判定 QX2*t*t + QX1*t + QX0 - rect.left = 0; (Y >= rect.top, Y <= rect.bottom, 0 <= t <= 1)
// 矩形の線分式2との判定 QX2*t*t + QX1*t + QX0 - rect.right = 0; (Y >= rect.top, Y <= rect.bottom, 0 <= t <= 1)
// 矩形の線分式3との判定 QY2*t*t + QY1*t + QY0 - rect.top = 0; (X >= rect.left, X <= rect.right, 0 <= t <= 1)
// 矩形の線分式4との判定 QY2*t*t + QY1*t + QY0 - rect.bottom = 0; (X >= rect.left, X <= rect.right, 0 <= t <= 1)
*/
// tについて解く。
//解の公式を使うために、a*t*t + b*t + c = 0;の形に整理し、定数a,b,cの値を定義する。
// 矩形の線分式1,2,3,4のtの解を求める定数abcのオブジェクトを、配列に格納する。
const abc = [
{a: qCurve.QX2, b: qCurve.QX1, c: qCurve.QX0 - rect.left} ,
{a: qCurve.QX2, b: qCurve.QX1, c: qCurve.QX0 - rect.right} ,
{a: qCurve.QY2, b: qCurve.QY1, c: qCurve.QY0 - rect.top} ,
{a: qCurve.QY2, b: qCurve.QY1, c: qCurve.QY0 - rect.bottom}
];
for(let i of abc) { //4辺それぞれの交点について、判定する。
const delta = i.b*i.b - 4*i.a*i.c;
const timeCurveCheck = []; //求めたtの解をチェックする配列
if (delta === 0) { timeCurveCheck.push( -i.b/(2*i.a) ); }
else if (delta > 0) {
timeCurveCheck.push( (-i.b + Math.sqrt(delta))/(2*i.a) );
timeCurveCheck.push( (-i.b - Math.sqrt(delta))/(2*i.a) );
}
for(let t of timeCurveCheck) { //tの解が交点であるかチェック
if(0 <= t && t <= 1){
if(i.b == qCurve.QX1) { const y3 = qCurve.fy(t); //tがX座標についての方程式の解なら、tを代入したY座標を調べる
if( rect.top <= y3 && y3 <= rect.bottom) { timeCurve.push(t);} //Y座標が線分の範囲なら判定OKリストに追加
}
else { const x3 = qCurve.fx(t); //tがY座標についての方程式の解なら、tを代入したX座標を調べる、
if( rect.left <= x3 && x3 <= rect.right) { timeCurve.push(t);} //X座標が線分の範囲なら判定OKリストに追加
}
}
}
}
if(timeCurve.length > 0) { return timeCurve; } // 交点(判定OK)となるtの解をリストで渡す(判定true)
else {return false;} // もし解が無ければ、false判定。
}
式の解説は、ソース内にコメントで書き残してます。辺それぞれとの判定が、直線との交差判定とほぼ同じです。
工夫としては、4辺の線分の解について配列[]を用い、計算式の行程を使いまわしてるくらいかな?

⇒ ベジェ曲線とキャラクター(矩形)の当たり判定デモを見る
デモにて、うまく判定できました。後はhit時のバウンス処理(法線ベクトル)を考えるかな。
2次ベジェ曲線にぶつかった時のバウンス判定
0から1の間で変化する変数tを用いた2次式の曲線で、ぶつかるポイントとなるtの値が判れば、そのまま法線ベクトルを求めることができます。2次曲線上の交点となるtが得られた時の法線ベクトルは?
当たった位置の法線は、二次ベジェ曲線の式をtで微分して接線を求め変形する。 x' = 2*(qCurve.x2 - 2*qCurve.cp1x + qCurve.x)*t + 2*(qCurve.cp1x - qCurve.x); y' = 2*(qCurve.y2 - 2*qCurve.cp1y + qCurve.y)*t + 2*(qCurve.cp1y - qCurve.y); 法線ベクトル = (-y', x')
参考 ⇒ 二次ベジェ曲線と線分の当たり判定
法線ベクトルを求める際のt値は当たり判定式で得られるのですが、このままだと値を別の関数(バウンス処理)に持ち越すことはできません... どうにか、hit判定=trueを返すときに、このtも渡すことができれば良いのですが...
当たり判定式で求めた解「t」を、この関数でも使いたい
そこで前準備として、2次曲線の当たり判定式(true or false)のreturnを、t値で渡すことができないか確かめてみます。 判定式をtrueでなく解として得られたt値を渡したとしても、そのt値がtrueとして認識してもらえるなら、hitイベントが問題なく起こるはずなのです!さ、当たり判定でtの解をそのまま渡せるかな?
参考 ⇒ [JavaScript] null とか undefined とか 0 とか 空文字('') とか false とかの判定について
あ、phinaさんの記事ですね。以前も矩形と円の当たり判定高速化のときにお世話になりました(o _ o。)
抜粋すると、オブジェクトや配列で値を返すとき、それはtrueで評価されるということ。
つまり、tの解を配列でそのまま渡せるということです!
注意点として値が0のときはfalseで評価される。解が0のとき、そのまま数値で渡すと思わぬ判定をされてしまう可能性。。。
そのため、配列で格納した状態で渡すのが安全かな?と思われます。(解が複数ある場合もあるし)
よって、2次曲線との衝突判定式で交点となる解(t)を配列でreturnできるように改良します。
tの解を返す2次曲線と線分の衝突判定式
deLineQCurve(line, qCurve) { //線分と2次ベジェ曲線の衝突判定式
if( !this.deRectLine(qCurve.aabbRect, line) ) {return false;} //2次曲線のaabb矩形と直線を判定して、falseならfalseを返して終了
//解の公式を使うために、a*t*t + b*t + c = 0;の形に整理し、定数a,b,cの値を定義する。
const a = line.dy* qCurve.QX2 - line.dx* qCurve.QY2;
const b = line.dy* qCurve.QX1 - line.dx* qCurve.QY1;
const c = line.dy* qCurve.QX0 - line.dx* qCurve.QY0 + line.dx*line.y - line.dy*line.x;
//解の公式 t = (-b ± Math.sqrt(b*b - 4*a*c))/(2*a)
//解の公式を用いて2次方程式の定数tの値(2つある)を得る判定
const delta = b*b - 4*a*c; //Math.sqrt(b*b - 4*a*c))の中身を判定
const timeCurveCheck = []; //求めたtの解をチェックする配列
if (delta < 0) {return false;} //delta が負に値になるとき、解はない。交点が存在しない
else if (delta === 0) { //delta=0 のとき、tの解は1つ。timeCurveCheckリストにtの解を一つ追加する
timeCurveCheck.push( -b/(2*a) ); //tの解 = -b/(2*a)
}
else if (delta > 0) { //delta>0 のとき、tの解は2つ。timeCurveCheckリストにtの解を二つ追加する
timeCurveCheck.push( (-b + Math.sqrt(delta))/(2*a) ); //tの解1つめ = -b + Math.sqrt(delta))/(2*a)
timeCurveCheck.push( (-b - Math.sqrt(delta))/(2*a) ); //tの解2つめ = -b - Math.sqrt(delta))/(2*a)
}
const timeCurve = []; //tの解で交点となるtの解答リスト
for(let t of timeCurveCheck) { //求めたtの解(timeCurveCheckリストに格納)それぞれについて判定
if(0 <= t && t <= 1){ /*tの解が0 <= t <=1 のとき、直線Lineとの交点を持つ。tを曲線上の式に代入した座標が線分上に存在するなら当たり!*/
if (line.x === line.x2 ) { const y3 = qCurve.fy(t); //交点のY座標を求める、直線のX座標が一定ならY座標判定へ
if ( line.y <= y3 && y3 <= line.y2 || line.y2 <= y3 && y3 <= line.y ) { timeCurve.push(t); } //Y座標が線分上にあるなら交点座標となるtを解答リストに追加!
}
else { const x3 = qCurve.fx(t); //交点のX座標を求める
if ( line.x <= x3 && x3 <= line.x2 || line.x2 <= x3 && x3 <= line.x ) { timeCurve.push(t); } //X座標が線分上にあるなら交点座標となるtを解答リストに追加!
}
}
}
if(timeCurve.length > 0) { return timeCurve; } // 交点(判定OK)となるtの解をリストで渡す(判定true)
else {return false;} // もし解が無ければ、false判定。
}
ま、こんなもんでしょ。QuadraticCurveクラスを改良したお陰でそこそこ簡略化できてます。
判定式にて、先に解を格納する配列const timeCurve = [];を用意しておく。 求めたtの解に対し、線分との交点がとれるかどうかチェックして、OKなら配列に追加。
returnで、解の配列を返す。
配列が空(timeCurve.length == 0)の場合、条件に合う解が存在しない。falseを返す。
これで、tの解が配列に格納された状態でreturnされます。
次に得られたtの解を、バウンス判定式に渡す方法について。
Sceneクラスにて、Hit判定式=true時の関数を見直す
Sceneクラスにて、hit判定式の結果を返してる部分。ゲーム作り5項で取り入れた4分木での当たり判定testの後は、2ヵ所存在してます。
Sceneクラスの_hitTest()内にて
const hit = this._detector.detectCollision(collider1, collider2);
if(hit) {
obj1.dispatchEvent('hit', new GameEvent(obj2));
obj2.dispatchEvent('hit', new GameEvent(obj1));
}
該当箇所を、こんな感じに修正します。
const hit = this._detector.detectCollision(collider1, collider2);
if(hit) {
obj1.dispatchEvent('hit', new GameEvent(obj2, hit));
obj2.dispatchEvent('hit', new GameEvent(obj1, hit));
}
これで衝突相手のオブジェクトだけでなく、hit判定で得られたreturnの値も渡せるようになりました。
GameEventクラスについて、見直し
それから、大元のGameEventクラス(addEventListenerに登録した関数に値を渡す役割)で指定できる要素は1つまででした。 e.targetで、衝突相手のobjectにアクセスできるのは、このクラスのお陰です。 従来は関数に渡す値を1つだけ設定してましたが、ここで二つ目の要素にも参照できるよう変更を加えます。GameEventクラスに2つ目の要素を追加する
class GameEvent {//dispatchEventにて、addEventListenerに登録した関数に値を渡す役割
constructor(target, info) {
this.target = target;
this.info = info;
}
}
addEventListenerの関数に渡されたeから、二つ目の要素(e.info)にアクセスできるようになりました。 これで、衝突判定で交点となるtの値も引き継げるようになります。
アクターと2次曲線との反動ベクトルを求める準備が整いました
下準備がとても長かったですね。ひとまずこれで必要な要素を揃えることができたと思います。後は計算の手順です。2次曲線との衝突判定にて反動ベクトルを考える
- 求まったt値のリストより、法線の単位ベクトルを求める。
- 後はラインとの衝突処理と同じ感覚で、アクターのspeedに単位ベクトルをかけて、X軸Y軸の移動距離に反映させる
たぶん、tの値(複数ある)から法線ベクトルを得るというのが、今回の新しいチャレンジとなりそうです。後はラインと同じ。
得られたtの値から法線ベクトルを求め、バウンド処理をする
では、アクターのaddEventListenerに、2次曲線とぶつかった時の反動処理を関数で登録します。 やりながら解説かいてみよ。得られたtの値を平均値でとる
接触判定時の2次曲線と矩形との交点は、1つだけとは限りません。 この図からもイメージできる通り、矩形との衝突時は最大で4つの交点があります。
...どの点で法線ベクトルをとればいいんだ? っていうの、これたぶんtの解の平均値でいんじゃないかな?って思うのです。 平均を取ると、だいたいその辺と接してるんだろ〜っていう起点となる場所が分かります。では、渡されたtの解(配列の中の値)を平均値で取得してみます。
参考 ⇒ Array.prototype.reduce()
配列のメソッドに用意されてる.reduce()という関数を用いる。 これによって、配列[0]から配列[1]、その結果に配列[2]、さらにその結果に配列[3]...と、配列が終わるまで全ての処理を順番に実行、結果を単一の値に上書きするような感覚でしょうか。 配列の中のすべてを足した値を返すのは、だいたいこんな描き方でよろしいようです。
複数あるtの解を合計値で取得
const tArray = e.info; //tの解のリストが格納された配列 const tSum = tArray.reduce((a, c) => a + c);
tの合計値をArray.lengthで割って、平均値を出す
const t = tSum / tArray.length; // tの解の平均値を得る、このtから法線ベクトルを求める
合計値をtSumという要素で求めたら、ここから平均値を出せます。合計数から足した回数で割ればOK。
得られたtの平均値から法線ベクトルを求める
とりあえずtが判ったので、法線ベクトルを求めてみましょう。当たった位置の法線は、二次ベジェ曲線の式をtで微分して接線を求め変形する。 x' = 2*(qCurve.x2 - 2*qCurve.cp1x + qCurve.x)*t + 2*(qCurve.cp1x - qCurve.x); y' = 2*(qCurve.y2 - 2*qCurve.cp1y + qCurve.y)*t + 2*(qCurve.cp1y - qCurve.y); 法線ベクトル = (-y', x')
参考 ⇒ 二次ベジェ曲線と線分の当たり判定
参考サイトさんによると、だいたいこんな感じのようです。
、
法線ベクトルを求める下書き
const dx = - y' = - 2*(qCurve.y2 - 2*qCurve.cp1y + qCurve.y)*t - 2*(qCurve.cp1y - qCurve.y); const dy = x' = 2*(qCurve.x2 - 2*qCurve.cp1x + qCurve.x)*t + 2*(qCurve.cp1x - qCurve.x); const bounceVect = new Vector2D (dx, dy);
うーん、これは2次曲線クラス(Collider)の方で、すぐ取り出せるように関数化しておいたほうが良さそうですね。
QuadraticCurveクラスにメソッドを追加
bounceVect(t) { // tのときの曲線上の点から法線ベクトルを求める
const dx = - 2* this.QY2*t - this.QY1;
const dy = 2* this.QX2*t + this.QX1;
return new Vector2D(dx, dy);
}
const bounceVect = other.bounceVect(t).normalVect;
という感じで、衝突相手の2次曲線を示す変数と、定義したtの値から法線ベクトル(今回は単位ベクトルで)を呼び出すことができます。
交点と、自分の座標の位置関係を調べる
さてこの法線ベクトルですが、正でとるか負でとるか、悩ましい感じです。 うーん、ここはtの交点を求めて、自分との位置関係をベクトルで表してみようと思います。const otherCx = other.fx(t), otherCy = other.fy(t); // 曲線上のバウンドの起点となるXとYの座標を求める const delta = new Vector2D (this.hitArea.cx - otherCx, this.hitArea.cy - otherCy); //バウンドの起点から自分の中心点までのベクトルで、お互いの位置関係を取得
あとは、法線ベクトルと位置関係deltaのベクトルを内積で判定して、正の値ならそのままだし、食い違ってたら法線ベクトルはマイナスでとる感じになるでしょう。
if(bounceVect.innerP(delta) < 0) {bounceVect.dx*=-1; bounceVect.dy*=-1;}
ここまで来れば簡単です。後はラインのときと同じように、このアクターの速さ分だけ単位ベクトルの方向に移動させればOK
if ( this.speed*this.speed < this.vector.length2 ) { speed = this.vector.length; } //もし自分の移動ベクトルが(押し戻しなどの影響で)自分の速度より大きくなってるなら、移動ベクトルの大きさを反動の大きさとする。
this._velocityX += speed * bounceVect.dx; //X軸の反動の大きさを反映
this._velocityY += speed * bounceVect.dy; //Y軸の反動の大きさを反映

⇒ ベジェ曲線とキャラクター(矩形)のバウンス判定デモを見る
後日のプログラム改良
3次曲線のコードを組んでる最中に、2次方程式の解の公式に、改善点が見つかりました。1次の係数が2の倍数になってると、より簡略化した解の式が得られます。
⇒ 2次方程式の解の公式二つ目
1次のtの係数を2の倍数にして定義すると?
fx(t) { return this.QX2*t*t + 2*this.QX1*t + this.x; }
fy(t) { return this.QY2*t*t + 2*this.QY1*t + this.y; }
こうすると、解の公式が簡略化出来そう...
2次曲線クラス(Collider)のコード改良後
class QuadraticCurve extends Collider { //当たり判定を2次曲線で扱うクラス、物体の放物線の軌道だったり力場を作ったりする。
constructor(x, y, x1, y1, x2, y2, tag) {
super('quadraticCurve', x, y, tag);
this.x1 = x1; //制御点1のx座標
this.y1 = y1; //制御点1のy座標
this.x2 = x2; //終着点のx座標
this.y2 = y2; //終着点のy座標
}
// 曲線上のX座標 = fx(t) = (this.x2 - 2*this.x1 + this.x)*t*t + 2*(this.x1 - this.x)*t + this.x;
// 曲線上のY座標 = fy(t) = (this.y2 - 2*this.y1 + this.y)*t*t + 2*(this.y1 - this.y)*t + this.y;
get QX2() { return this.x2 - 2*this.x1 + this.x; } // 曲線上のX座標を求める方程式のt**2の係数
get QX1() { return this.x1 - this.x; } // 曲線上のX座標を求める方程式のt**1の係数の半分...使う時は2*QX1として使う。
get QY2() { return this.y2 - 2*this.y1 + this.y; } // 曲線上のY座標を求める方程式のt**2の係数
get QY1() { return this.y1 - this.y; } // 曲線上のY座標を求める方程式のt**1の係数の1/2...使う時は2*QY1として使う。
/* 2次ベジェ曲線の方程式(0 <= t <=1) t地点の座標を求める*/
fx(t) { return this.QX2*t*t + 2*this.QX1*t + this.x; }
fy(t) { return this.QY2*t*t + 2*this.QY1*t + this.y; }
/* 2次曲線の微分式(0 <= t <=1) の時の、曲線の傾きを求める */
f1x(t) { return 2*(this.QX2*t + this.QX1); }
f1y(t) { return 2*(this.QY2*t + this.QY1); }
//〜〜
数式をこのように定義し直す。すると。。。
直線と2次曲線との交点を求める数式が簡略化する
deLineQCurve(line, qCurve) { //線分と2次ベジェ曲線の衝突判定式
if( !this.deRectLine(qCurve.aabbRect, line) ) {return false;} //2次曲線のaabb矩形と直線を判定して、falseならfalseを返して終了
//解の公式を使うために、a*t*t + 2*b*t + c = 0;の形に整理し、定数a,b,cの値を定義する。
const a = line.dy* qCurve.QX2 - line.dx* qCurve.QY2;
const b = line.dy* qCurve.QX1 - line.dx* qCurve.QY1;
const c = line.dy* qCurve.x - line.dx* qCurve.y + line.dx*line.y - line.dy*line.x;
//解の公式Ⅱ t = (-b ± Math.sqrt(b*b - a*c))/a
//解の公式Ⅱを用いて2次方程式の定数tの値(2つある)を得る判定
const delta = b*b - a*c; //Math.sqrt(b*b - a*c))の中身を判定
const timeCurveCheck = []; //求めたtの解をチェックする配列
if (delta < 0) {return false;} //delta が負に値になるとき、解はない。交点が存在しない
else if (delta === 0) { //delta=0 のとき、tの解は1つ。timeCurveCheckリストにtの解を一つ追加する
timeCurveCheck.push( -b/a ); //tの解 = -b/a
}
else if (delta > 0) { //delta>0 のとき、tの解は2つ。timeCurveCheckリストにtの解を二つ追加する
const sqrtDelta = Math.sqrt(delta);
timeCurveCheck.push( (-b + sqrtDelta)/a ); //tの解1つめ = -b + Math.sqrt(delta))/a
timeCurveCheck.push( (-b - sqrtDelta)/a ); //tの解2つめ = -b - Math.sqrt(delta))/a
}
const timeCurve = []; //tの解で交点となるtの解答リスト
for(let t of timeCurveCheck) { //求めたtの解(timeCurveCheckリストに格納)それぞれについて判定
if(0 <= t && t <= 1){ /*tの解が0 <= t <=1 のとき、直線Lineとの交点を持つ。tを曲線上の式に代入した座標が線分上に存在するなら当たり!*/
if (line.x === line.x1 ) { const y3 = qCurve.fy(t); //交点のY座標を求める、直線のX座標が一定ならY座標判定へ
if ( line.y <= y3 && y3 <= line.y1 || line.y1 <= y3 && y3 <= line.y ) { timeCurve.push(t); } //Y座標が線分上にあるなら交点座標となるtを解答リストに追加!
}
else { const x3 = qCurve.fx(t); //交点のX座標を求める
if ( line.x <= x3 && x3 <= line.x1 || line.x1 <= x3 && x3 <= line.x ) { timeCurve.push(t); } //X座標が線分上にあるなら交点座標となるtを解答リストに追加!
}
}
}
if(timeCurve.length > 0) { return timeCurve; } // 交点(判定OK)となるtの解をリストで渡す(判定true)
else {return false;} // もし解が無ければ、false判定。
}
tの解を求める計算途中、余計な割り算掛け算を省けます(' '*)♪。
矩形との判定も同様に改良して、いい感じになりそうですね。
では、ここからさらに発展して、より実用的な3次曲線の当たり判定に入っていきます!(コスト大きいので注意) ⇒ JavaScriptでゲーム作り「10EX:3次曲線の当たり判定」
古都さんのフレームワークを元にほぼ最初から作ってます。
たぶん順番に見ないとちんぷんかんぷん(' '*)...
すぺしゃるさんくす
https://sbfl.net/古都さん
JavaScriptで作る弾幕STGの基礎(フレームワーク)を使わせていただいてます。感謝!

ぴぽやさんもありがとう、キャラチップをお借りしています。